Так почему всё же невозможно создание вечного двигателя на принципе "трубки Вентури"?

В статье "Гидравлический энергетический парадокс" я рассказал о многократном (в десятки и сотни раз) увеличении кинетической энергии* потока безо всяких дополнительных затрат энергии и безо всяких дополнительных воздействий на поток внешними силами.

* Имеется в виду ошибочная кинетическая энергия имени Лейбница, mV^2/2 а не правильная - Ньютона, mV.

И в конце этой статьи я задал довольно простой вопрос:

2. И почему всё же невозможно создание вечного двигателя на принципе "трубки Вентури"? Ведь халявное многократное, в десятки и даже сотни раз увеличение кинетической энергии имени Лейбница в узкой части трубки Вентури - налицо! Кое-кто из моих читателей уже "нащупал" правильный ответ, но вот привитый им в школе стереотип про закон сохранения энергии не даёт им возможности правильно сформулировать этот ответ.

К сожалению, ни одного достаточно вразумительного ответа на этот вопрос я так и не услышал, хотя статью прочитало до конца уже более 6,5 тыс. человек. Так как физикой сейчас вообще мало кто интересуется, молодёжь больше по смартфонам, по спорту, да по сексу - это три огромных "С", на которых стоит мир нового поколения, давно перешагнувшего через generation "П"епси (по Пелевину), а большинство из generation "П", к которому принадлежат и сам Виктор Пелевин, я, большинство профессоров и академиков ОФН РАН, и даже Медведев с Путиным (generation "Пу"?) чаще всего, судя по комментариям, школьную физику тоже не очень хорошо знало, да еще и подзабыло, то такое кол-во просмотров чисто физической статьи меня порадовало.

Поэтому я решил слегка подучить и поколение "П", и поколение "трёх С" в плане понимания реальной физики, в частности - гидравлики.

Итак, почему же невозможен вечный двигатель на принципе "трубки Вентури", хотя мы там наблюдаем бешеный халявный прирост энергии имени Лейбница.

Смотрим на рисунок:

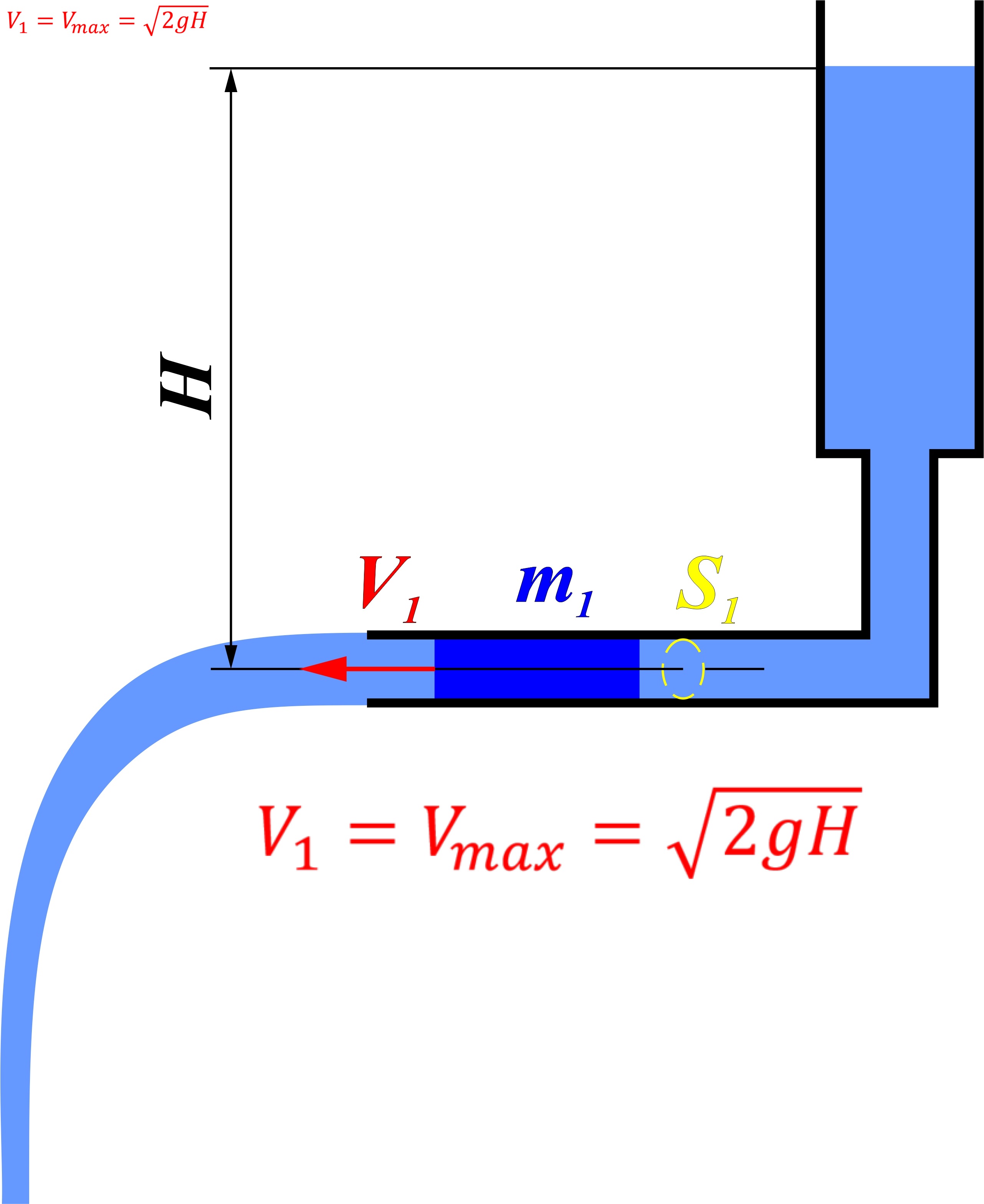
Рисунок 1. Скорость потока жидкости зависит лишь от давления - в данном случае - гидростатического.

На рисунке 1 показано, как из некоей емкости вытекает "идеальная" жидкость, пусть это будет ламинарный поток воды. Из школьной программы физики (я не отрицаю всю школьную программу физики - я просто пытаюсь обратить внимание на тот факт, что в школьной физике есть существенные и даже фундаментальные заблуждения и ошибки) известно, что максимальная скорость потока определяется лишь величиной разности давлений, в данном случае эта разность, после сокращения атмосферного давления, равна гидростатическому давлению (ро - это плотность жидкости) (po) * g * H. Соответственно, выводится, что V_1 = V_max = SQRT(2gH). (SQRT - это квадратный корень, если кто не знает)

Труба постоянного диаметра, с отверстием площадью S_1. При этом через любое сечение (допустим, что уровень воды в емкости постоянно пополняется до родной и той же отметки) через которое в единицу времени (допустим, в одну секунду) проходит количество жидкости, равное m_1 = (ро) * S_1 * V_1.

Но вот мы решили сузить диаметр трубы, рассчитывая получить потрясающий прирост халявной энергии для изготовления вечного двигателя. Допустим, мы уменьшили диаметр трубы в 3 раза. При этом площадь сечения в узком участке трубы уменьшилась в 9 раз^ S_2 = S_1 / 9.

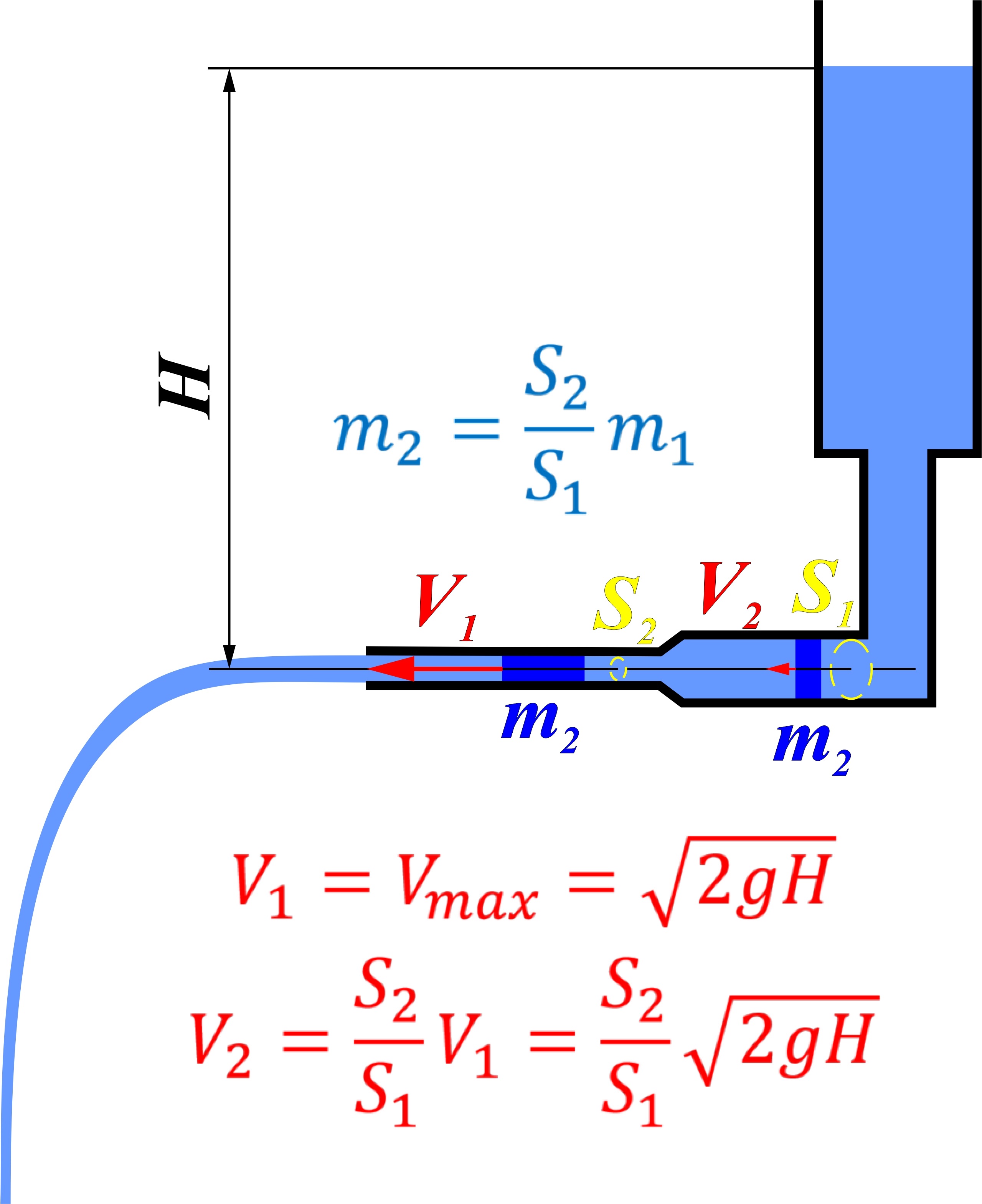
Рис. 2. Печальная правда о трубке Вентури.

Почему же не получился у Данилы-мастера каменный цветок? Почему трубка Вантури не позволила сделать вечный двигатель? Прежде всего, по той простой причине, что максимальная скорость потока воды осталась прежней V_1 - так как V_1 = V_max = SQRT(2gH), но при этом величина потока, то есть кол-во молекул воды, проскакивающих через то или иное сечение в любом участке трубы уменьшилось в 9 раз: m_2 = m_1 / 9.

Соответственно, скорость потока в широкой части трубы уменьшилась в те же самые 9 раз: V_2 = V_1 / 9. Таким образом, чтобы получить поток такой же мощности, как и на рис. 1, необходимо установить 9 таких труб переменного сечения, как на рис. 2.

ОДНАКО !!!

Этот факт не отрицает того, что кинетическая энергия имени Лейбница, КЭ(Л), на втором рисунке совершенно халявным образом увеличилась ровнёхонько в 81 раз:

в сечении S_1: КЭ(Л)_1 = m_2 * (V_2)^2 / 2

в сечении S_2: КЭ(Л)_2 = m_2 * (V_1)^2 / 2 = m_2 * (9 * V_2)^2 / 2 = 81 * m_2 * (V_2)^2 / 2 = 81 * КЭ(Л)_1

В чем же дело? Как разрешить этот энергетический парадокс, который противоречит закону сохранения энергии, придуманной Лейбницем?

Ведь ВАЖНОСТЬ ПАРАДОКСОВ В НАУКЕ обусловлена тем, что "Современные науки, использующие логику в качестве инструмента познания, нередко наталкиваются на теоретические противоречия либо на противоречия теории опыту. Это бывает обусловлено неверной аксиоматизацией теорий, логическими ошибками в построении суждений, несовершенством существующих в настоящее время научных методов или недостаточной точностью используемых в опытах инструментов. Наличие парадокса стимулирует к новым исследованиям, более глубокому осмыслению теории, её «очевидных» постулатов и нередко приводит к полному её пересмотру."

Из гидравлического энергетического парадокса следует, что какую-то теорию необходимо пересматривать.

Многие остолопы этого до сих пор не поняли и пытаются встать своей впалой грудью и хилыми мозгами на защиту ошибочного догмата, придуманного Готтфридом Лейбницем.

Очень многие остолопы кинулись "опровергать" меня, указывая, что я не посчитал потенциальную энергию потока жидкости в трубе. Например, некий Борис Николаевич Барсуков заявил мне: "Бернулли в 19 веке знал что полная энергия складывается из потенциальной и кинетической, -одна убывает когда другая увеличивается.

Петр Иванович Дубровский, добросовестный инженер – исследователь, честный и непредвзятый частный научный детектив этого не знает в 21 веке :-)" Примерно в том же духе высказалось уже несколько остолопов, поэтому я решил ответить на эту довольно глупую "критику".

Вообще-то потенциальная энергия потока воды (я имею в виду удельную потенциальную энергию, равно как и, говоря про кинетическую энергию потока воды, я всегда имел в виду удельную кинетическую энергию) в ГОРИЗОНТАЛЬНОЙ трубе даже при переменном сечении трубы всегда одинакова. Так что истошные вопли остолопов, вроде бы как ходивших когда-то на уроки физики, но так и не понявших сути того, о чём я говорю, не должны смущать остальных читателей.

Возможно, остолопы имеют какое-то другое видение "потенциальной энергии потока"? Не знаю. Я каждого остолопа, написавшего мне о неучтённой мной "потенциальной энергии" попросил подтвердить свои бестолковые объяснения хотя бы элементарными расчётами. Всего-то и надо, что найти пропажу (или превращение) потенциальной энергии при переходе из широкого участка трубы в узкий, равную 80 (восьмидесяти) КЭ(Л)_1. То есть остолопам следует доказать, что ПЭ(Л)_1 = 81 * ПЭ(Л)_2.

Дерзайте. Но вот печалька - никто пока не дерзнул... Если кто, например, "умнейший и образованнейший" Борис Николаевич Барсуков, который почему-то и зачем-то переселил Даниила Бернулли (или Иоганна Бернулли, кто ж знает?) из XVIII века в 19-ый, сделает такой расчёт - пришлите мне, можно на e-mail d-pi@yandex.ru. Я опубликую. И - проверю. И обязательно макну остолопа в его умственные какашки.

На самом же деле, если воспользоваться правильным понятием "энергии", в частности, правильным понятием кинетической энергии (mV) на основе второго закона Ньютона - КЭ(Н), то в этом случае правильный закон сохранения энергии** ΔКЭ(Н) = ΔmV = Ft - работает.

** Ныне этот правильные закон сохранения энергии известен как закон сохранения импульса.

---

Ну-ка, ну-ка, а разве работает? Давайте проверим, смотрим на рисунок 2:

В сечении S_1 : КЭ(Н)_1 = m_2 * V_2

В сечении S_2 : КЭ(Н)_2 = m_2 * V_1 = m_2 * (9 * V_2) = 9 * КЭ(Н)_1

Божечки, и тут наблюдается "халявное" увеличение кинетической энергии, на этот раз - "правильной" кинетической энергии имени Ньютона. Правда, не столь впечатляющее, не в десятки и сотни раз,... но всё же!!!

Снова парадокс?

Есть у кого какие идеи, как разрешить этот парадокс?

Как-нибудь я расскажу о том, как разрешить этот парадокс - сперва хочу послушать мнение умных читателей. Да, остолопам напоминаю, что иногда лучше промолчать - тогда можно хотя бы сойти за умного, а не за Бориса Николаевича Барсукова.

Как всё-таки был прав человек, придумавший, будто бы что царь Петр Первый указал, что "боярам в Думе говорить по ненаписанному, дабы дурь каждого видна была видна". Я пока так и не нашёл документального подтверждения, что Пётр Первый когда-то либо говорил, либо подписал Царский Указ такого содержания... но дурь остолопов совершенно замечательно видна по их комментариям.