Миролюбивые шахматные кони.

                                       Задача                           

                                         Рис. 1.

Клетки доски 5×5 раскрашены в шахматном порядке (рис. 1).

 а) Какое наибольшее число шахматных коней можно расставить на этой доске так, чтобы они не били друг друга?

 б) Сколькими способами это можно сделать?

(обязательно будут, но позже, а пока есть время для дерзаний

Подсказка.

Кони,стоящие на одной диагонали, друг друга не бьют.

Решение.

Расстановка 13 коней показана слева на рис. 2. Докажем, что большее число не бьющих друг друга коней расставить на такой доске нельзя. Для этого мысленно разобьем клетки на пары так, чтобы в каждую пару входили клетки, отстоящие друг от друга на один ход коня. Одной клетке, естественно, пары не найдется. В том, что такое разбиение существует, можно убедиться, посмотрев на правую часть рис. 2.

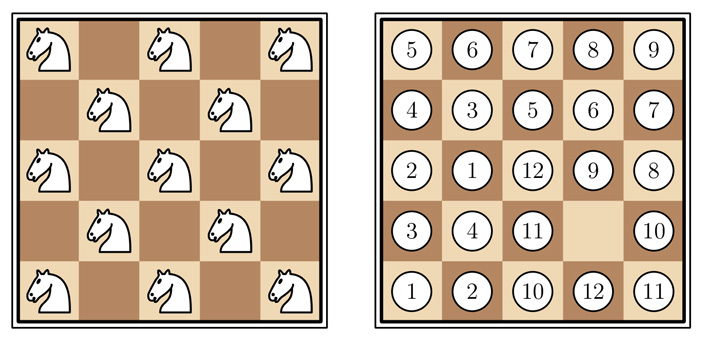
Рис. 2.

Очевидно, что, как ни расставляй коней на доске, в каждой паре можно будет занять не больше одной клетки. Это означает, что коней заведомо не больше, чем количество пар, которых 12, плюс один (одна непарная клетка) — то есть 13.

Чтобы показать, что расстановка 13 коней на этой доске всего одна, идею с разбиением клеток на пары удобно несколько модифицировать.

Рассмотрим граф, вершинами которого будут центры клеток доски. Две вершины соединим ребром, если из одной в другую можно попасть за один ход коня. Этот граф показан слева на рис. 3. Важно, что в этом графе есть последовательность ребер, которая проходит через каждую из 25 вершин ровно по одному разу (рис. 3, справа).

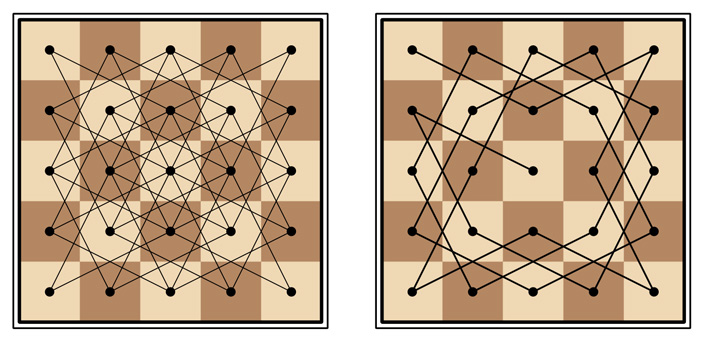
Рис. 3.

На языке теории графов последовательности вершин, соединенных по цепочке ребрами, называют путями. Ясно, что из любых двух клеток, которые встречаются подряд на нашем пути, конь может стоять только в одной. Поэтому для того, чтобы «уместить» максимальное число коней, начинать надо прямо с первой клетки этого пути. Это и даст расстановку, показанную на рис. 2.

Послесловие.

Рис. 4. Уильям Гамильтон, фотопортрет середины XIX века. Изображение из твиттера библиотеки Дублинского университета

Путь в графе, который помог нам решить задачу, проходил через все вершины графа по одному разу. Такие пути называются гамильтоновыми. Если в графе есть замкнутый гамильтонов путь (у которого совпадают начало и конец, путь в таком случае является циклом), то сам граф называется гамильтоновым. Название дано в честь ирландского математика Уильяма Гамильтона (1805–1865), которого по праву называют одним из величайших математиков XIX столетия: он оставил значительный вклад в разных областях математики (про некоторые важнейшие разделы вообще можно сказать, что они впоследствии выросли из его работ), механики и оптики.

Известно, что по мотивам своих исследований Гамильтон даже придумал игру-головоломку «Икосиан» (осторожно: перейдя по этой ссылке вы увидите решение головоломки!), которая одно время продавалась и была довольно популярной. Цель игры — построить гамильтонов цикл (то есть пройти по всем вершинам, каждый раз переходя в соседнюю по ребру, и вернуться в начало пути) в правильном додекаэдре (рис. 5, слева). Поскольку изготавливать такой правильный многогранник, а затем распространять его и, главное, играть с ним не очень удобно, игра представляла собой плоскую доску с выемками для фишек, соединенными линиями, соответствовавшими ребрам додекаэдра (рис. 5, справа). Фишек было 20 (столько же, сколько вершин у додекаэдра), они были пронумерованы, чтобы их можно было расставлять в порядке обхода.

Рис. 5. Додекаэдр и игра «Икосиан»

Рис. 5. Слева: додекаэдр — один из пяти правильных многогранников; у него 12 граней, являющихся одинаковыми правильными пятиугольниками, 30 ребер и 20 вершин. Рисунок с сайта ru.wikipedia.org. Справа: оригинальный экземпляр игры «Икосиан». Любопытно, что игра названа «в честь» икосаэдра, а обходить в ней надо додекаэдр. Связано это с тем, что эти два многогранника двойственны друг другу Фото с сайта researchgate.net

В задаче о гамильтоновом пути требуется выяснить, есть ли в данном графе гамильтонов путь (или цикл), и, в случае положительного ответа, найти его явно. Эта задача — важная и неожиданно сложная с точки зрения сложности вычислений: в известных алгоритмах с ростом числа вершин в графе количество требуемых операций растет экспоненциально. Из-за этого такие алгоритмы на практике неэффективны: фактически для произвольного графа с сотней-другой вершин уже невозможно получить ответ на этот вопрос даже на самом мощном суперкомпьютере. По сути, эти алгоритмы — хоть и оптимизированный, но перебор всех возможных путей.

При этом, если кто-нибудь предоставит вам сколь угодно большой и сложный граф, а также путь в нем, то проверить, является ли этот конкретный путь гамильтоновым, вы сможете довольно просто. Это (вместе с тем, что пока неизвестен быстрый алгоритм решения) означает, что с точки зрения теории алгоритмов задача о гамильтоновом пути попадает в класс сложности NP. Более того, она является NP-полной задачей: к ней относительно просто — за полиномиальное время — можно свести любую другую задачу из этого класса. Раз уж зашла речь об классах сложности, то нельзя не упомянуть одну из так называемых задач тысячелетия — проблему равенства классов P и NP. К классу P относятся задачи, для которых известны алгоритмы, в которых количество операций растет как какой-то определенный многочлен от размера входных данных. Даже если степень многочлена большая, с точки зрения теории алгоритмов такая задача считается простой. Если придумать полиномиальный алгоритм для любой NP-полной задачи (в том числе и для поиска гамильтонова пути), то эта проблема автоматически будет решена.

При этом с «теоретической» точки зрения про гамильтоновы пути известно, грубо говоря, всё, поскольку теорема Бонди — Хватала (Bondy–Chvátal theorem) дает критерий того, что граф является гамильтоновым: для этого необходимо и достаточно, чтобы замыкание этого графа тоже было гамильтоновым графом. Замыкание графа G с n вершинами — это граф, который строится последовательным «пририсовыванием» ребер, соединяющих любую пару вершин, удовлетворяющую следующим двум свойствам: во-первых, эти вершины должны быть еще не соединены ребром, а во-вторых, сумма их степеней должна быть больше n. Проблема с этой теоремой в том, что она не помогает в алгоритмическом поиске гамильтонова цикла. И даже просто для ответа на вопрос о том, есть ли в графе такой цикл, она плохо годится, поскольку сводит проверку одного графа к проверке другого, в котором к тому же больше ребер. Исключение — те случаи, когда замыкание графа оказывается «хорошим»: про него относительно легко понять, что он гамильтонов. Пример «хорошего» в этом смысле графа — полный граф, в котором любые две вершины соединены ребрами (при n>2 он точно гамильтонов).

Рис. 6. Леонард Эйлер. Портрет, выполненный Я. Э. Хандманном (1756 год). Рисунок с сайта ru.wikipedia.org

Кстати, с другим важным типом путей в графах — эйлеровыми путями, которые проходят по одному разу по всем ребрам, — все гораздо проще. Во-первых, есть простой критерий эйлеровости графа: связный граф эйлеров (то есть в нем есть эйлеров цикл) тогда и только тогда, когда в нем нет вершин нечетной степени. Во-вторых, есть алгоритмы, которые ищут такие пути за линейное время от размера графа (количества ребер). Понятие эйлерова пути появилось, когда Леонард Эйлер размышлял над задачей о семи кёнигсбергских мостах (это было в районе 1736 года).

Охватить весь спектр приложений эйлеровых и гамильтоновых графов в рамках нашей статьи невозможно, но можно посоветовать заинтересовавшимся читателям ознакомиться, например, со статьей Ф. Компо и П. Певзнера «Реконструкция генома: головоломка из миллиарда кусочков» («Квант», №3 за 2014 год). В ней подробно описано, какие математические идеи лежат в основе методов секвенирования ДНК и, в том числе, какую роль играют в этом эйлеровы и гамильтоновы графы.

Вернемся к приключениям шахматного коня на доске. Вспомним, что в решении задачи мы рассмотрели «коневой» граф шахматной доски 5×5 (он нарисован слева на рис. 3) и нашли в нем гамильтонов путь. По сути, этот путь показывает, как можно шахматным конем обойти всю доску, побывав в каждой клетке ровно один раз. Оказывается, этот вопрос — можно ли обойти конем данную доску (не обязательно квадратную)? — известен не одну сотню лет. Распространенное название — задача о ходе коня (Knight's tour).

Легко видеть (на примере нашей задачи), что это частный случай поиска гамильтонова пути. Благодаря специфике «коневого» графа он решается относительно просто. Одно из первых исследований этого вопроса, кстати, выполнил Эйлер: в статье Solution d'une question curieuse qui ne paroît soumise à aucune analyse (1759 год) он предложил способ строить нужные обходы коня для доски 8×8.

С тех пор, разумеется, этот вопрос изучен вдоль и поперек. Например, известно, что всего для обычной шахматной доски существует 13 267 364 410 532 замкнутых обходов. Придуманы разные алгоритмы построения нужного пути. Самый, пожалуй, простой формулируется буквально одной фразой: нужно начать из любой клетки и каждым ходом ходить в ту клетку, с которой потом можно попасть на минимальное число еще не пройденных клеток (если таких клеток несколько, то можно выбрать любую). Этот способ называется правилом Варнсдорфа, он был предложен еще в XIX веке. Уточнение, написанное в скобках, делать приходится, потому что описанные в нем ситуации вполне вероятны и нужно хоть как-то выбирать из равнозначных вариантов. При внимательном исследовании этого способа (уже при помощи компьютеров) оказалось, что иногда совсем произвольный выбор следующей клетки для хода коня может впоследствии завести его в тупик. Однако это происходит довольно редко. Подробнее об этом рассказано в книге Е. Гика «Шахматы и математика».

Источник