Если в результате прочтения этой подборки вы не запутаетесь полностью, значит вы мыслите недостаточно ясно

Учёные и мыслители с давних времён любят развлекать себя и коллег постановкой неразрешимых задач и формулированием разного рода парадоксов. Некоторые из подобных мысленных экспериментов сохраняют актуальность на протяжении тысяч лет, что свидетельствует о несовершенстве многих популярных научных моделей и «дырах» в общепринятых теориях, давно считающихся фундаментальными. Предлагаем вам поразмыслить над наиболее интересными и удивительными парадоксами, которые, как сейчас выражаются, «взорвали мозг» не одному поколению логиков, философов и математиков.

1. Апория «Ахиллес и черепаха»

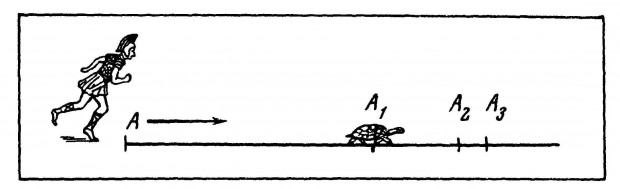
Парадокс Ахиллеса и черепахи — одна из апорий (логически верных, но противоречивых высказываний), сформулированных древнегреческим философом Зеноном Элейским в V-м веке до нашей эры. Суть её в следующем: легендарный герой Ахиллес решил посоревноваться в беге с черепахой. Как известно, черепахи не отличаются прыткостью, поэтому Ахиллес дал сопернику фору в 500 м. Когда черепаха преодолевает эту дистанцию, герой пускается в погоню со скоростью в 10 раз большей, то есть пока черепаха ползёт 50 м, Ахиллес успевает пробежать данные ей 500 м форы. Затем бегун преодолевает следующие 50 м, но черепаха в это время отползает ещё на 5 м, кажется, что Ахиллес вот-вот её догонит, однако соперница всё ещё впереди и пока он бежит 5 м, ей удаётся продвинуться ещё на полметра и так далее. Дистанция между ними бесконечно сокращается, но по идее, герою так и не удаётся догнать медлительную черепаху, она ненамного, но всегда опережает его.

Конечно, с точки зрения физики парадокс не имеет смысла — если Ахиллес движется намного быстрее, он в любом случае вырвется вперёд, однако Зенон, в первую очередь, хотел продемонстрировать своими рассуждениями, что идеализированные математические понятия «точка пространства» и «момент времени» не слишком подходят для корректного применения к реальному движению. Апория выявляет расхождение между математически обоснованной идеей, что ненулевые интервалы пространства и времени можно делить бесконечно (поэтому черепаха должна всегда оставаться впереди) и реальностью, в которой герой, конечно, выигрывает гонку.

2. Парадокс временной петли

Парадоксы, описывающие путешествия во времени, давно служат источником вдохновения для писателей-фантастов и создателей научно-фантастических фильмов и сериалов. Существует несколько вариантов парадоксов временной петли, один из самых простых и наглядных примеров подобной проблемы привёл в своей книге «The New Time Travelers» («Новые путешественники во времени») Дэвид Туми, профессор из Университета Массачусетса.

Представьте себе, что путешественник во времени купил в книжном магазине экземпляр шекспировского «Гамлета». Затем он отправился в Англию времён Королевы-девы Елизаветы I и отыскав Уильяма Шекспира, вручил ему книгу. Тот переписал её и издал, как собственное сочинение. Проходят сотни лет, «Гамлета» переводят на десятки языков, бесконечно переиздают, и одна из копий оказывается в том самом книжном магазине, где путешественник во времени покупает её и отдаёт Шекспиру, а тот снимает копию и так далее… Кого в таком случае нужно считать автором бессмертной трагедии?

3. Парадокс девочки и мальчика

В теории вероятностей этот парадокс также называют «Дети мистера Смита» или «Проблемы миссис Смит». Впервые он был сформулирован американским математиком Мартином Гарднером в одном из номеров журнала «Scientific American». Учёные спорят над парадоксом уже несколько десятилетий и существует несколько способов его разрешения. Поразмыслив над проблемой, вы можете предложить и свой собственный вариант.

В семье есть двое детей и точно известно, что один из них — мальчик. Какова вероятность того, что второй ребёнок тоже имеет мужской пол? На первый взгляд, ответ вполне очевиден — 50 на 50, либо он действительно мальчик, либо девочка, шансы должны быть равными. Проблема в том, что для двухдетных семей существует четыре возможных комбинации полов детей — две девочки, два мальчика, старший мальчик и младшая девочка и наоборот — девочка старшего возраста и мальчик младшего. Первую можно исключить, так как один из детей совершенно точно мальчик, но в таком случае остаются три возможных варианта, а не два и вероятность того, что второе чадо тоже мальчик — один шанс из трёх.

4. Парадокс Журдена с карточкой

Проблему, предложенную британским логиком и математиком Филиппом Журденом в начале XX-го века, можно считать одной из разновидностей знаменитого парадокса лжеца.

Представьте себе — вы держите в руках открытку, на которой написано: «Утверждение на обратной стороне открытки истинно». Перевернув открытку, вы обнаруживаете фразу «Утверждение на другой стороне ложно». Как вы понимаете, противоречие налицо: если первое утверждение правдиво, то второе тоже соответствует действительности, но в таком случае первое должно оказаться ложным. Если же первая сторона открытки лжива, то фразу на второй также нельзя считать истинной, а это значит, первое утверждение опять-таки становится правдой… Ещё более интересный вариант парадокса лжеца — в следующем пункте.

5. Софизм «Крокодил»

На берегу реки стоят мать с ребёнком, вдруг к ним подплывает крокодил и затаскивает ребёнка в воду. Безутешная мать просит вернуть её чадо, на что крокодил отвечает, что согласен отдать его целым и невредимым, если женщина правильно ответит на его вопрос: «Вернёт ли он её ребёнка?». Понятно, что у женщины два варианта ответа — да или нет. Если она утверждает, что крокодил отдаст ей ребёнка, то всё зависит от животного — посчитав ответ правдой, похититель отпустит ребёнка, если же он скажет, что мать ошиблась, то ребёнка ей не видать, согласно всем правилам договора.

Отрицательный ответ женщины всё значительно усложняет — если он оказывается верным, похититель должен выполнить условия сделки и отпустить дитя, но таким образом ответ матери не будет соответствовать действительности. Чтобы обеспечить лживость такого ответа, крокодилу нужно вернуть ребёнка матери, но это противоречит договору, ведь её ошибка должна оставить чадо у крокодила.

Стоит отметить, что сделка, предложенная крокодилом, содержит логическое противоречие, поэтому его обещание невыполнимо. Автором этого классического софизма считается оратор, мыслитель и политический деятель Коракс Сиракузский, живший в V-м веке до нашей эры.

6. Апория «Дихотомия»

Ещё один парадокс от Зенона Элейского, демонстрирующий некорректность идеализированной математической модели движения. Проблему можно поставить так — скажем, вы задались целью пройти какую-нибудь улицу вашего города от начала и до конца. Для этого вам необходимо преодолеть первую её половину, затем половину оставшейся половины, далее половину следующего отрезка и так далее. Иначе говоря — вы проходите половину всего расстояния, затем четверть, одну восьмую, одну шестнадцатую — количество уменьшающихся отрезков пути стремится к бесконечности, так как любую оставшуюся часть можно разделить надвое, значит пройти весь путь целиком невозможно. Формулируя несколько надуманный на первый взгляд парадокс, Зенон хотел показать, что математические законы противоречат реальности, ведь на самом деле вы можете без труда пройти всё расстояние без остатка.

7. Апория «Летящая стрела»

Знаменитый парадокс Зенона Элейского затрагивает глубочайшие противоречия в представлениях учёных о природе движения и времени. Апория сформулирована так: стрела, выпущенная из лука, остаётся неподвижной, так как в любой момент времени она покоится, не совершая перемещения. Если в каждый момент времени стрела покоится, значит она всегда находится в состоянии покоя и не движется вообще, так как нет момента времени, в который стрела перемещается в пространстве.

Выдающиеся умы человечества веками пытаются разрешить парадокс летящей стрелы, однако с логической точки зрения он составлен абсолютно верно. Для его опровержения требуется объяснить, каким образом конечный временной отрезок может состоять из бесконечного числа моментов времени — доказать это не удалось даже Аристотелю, убедительно критиковавшему апорию Зенона. Аристотель справедливо указывал, что отрезок времени нельзя считать суммой неких неделимых изолированных моментов, однако многие учёные считают, что его подход не отличается глубиной и не опровергает наличие парадокса. Стоит отметить, что постановкой проблемы летящей стрелы Зенон стремился не опровергнуть возможность движения, как таковую, а выявить противоречия в идеалистических математических концепциях.

8. Парадокс Галилея

В своём труде «Беседы и математические доказательства, касающиеся двух новых отраслей науки» Галилео Галилей предложил парадокс, демонстрирующий любопытные свойства бесконечных множеств. Учёный сформулировал два противоречащих друг другу суждения. Первое: есть числа, представляющие собой квадраты других целых чисел, например 1, 9, 16, 25, 36 и так далее. Существуют и другие числа, у которых нет этого свойства — 2, 3, 5, 6, 7, 8, 10 и тому подобные. Таким образом, общее количество точных квадратов и обычных чисел должно быть больше, чем количество только точных квадратов. Второе суждение: для каждого натурального числа найдётся его точный квадрат, а для каждого квадрата существует целый квадратный корень, то есть, количество квадратов равно количеству натуральных чисел.

На основании этого противоречия Галилей сделал вывод, что рассуждения о количестве элементов применены только к конечным множествам, хотя позже математики ввели понятие, мощности множества — с его помощью была доказана верность второго суждения Галилея и для бесконечных множеств.

9. Парадокс мешка картофеля

Допустим, у некоего фермера имеется мешок картофеля весом ровно 100 кг. Изучив его содержимое, фермер обнаруживает, что мешок хранился в сырости — 99% его массы составляет вода и 1% остальные вещества, содержащиеся в картофеле. Он решает немного высушить картофель, чтобы содержание воды в нём снизилось до 98% и переносит мешок в сухое место. На следующий день оказывается, что, один литр (1 кг) воды действительно испарился, но вес мешка уменьшился со 100 до 50 кг, как такое может быть? Давайте посчитаем — 99% от 100 кг это 99 кг, значит соотношение массы сухого остатка и массы воды изначально было равно 1/99. После сушки вода насчитывает 98% от общей массы мешка, значит соотношение массы сухого остатка к массе воды теперь составляет 1/49. Так как масса остатка не изменилась, оставшаяся вода весит 49 кг.

Конечно, внимательный читатель сразу обнаружит грубейшую математическую ошибку в расчётах — мнимый шуточный «парадокс мешка картофеля» можно считать отличным примером того, как с помощью на первый взгляд «логичных» и «научно подкреплённых» рассуждений можно буквально на пустом месте выстроить теорию, противоречащую здравому смыслу.

10. Парадокс воронов

Проблема также известна, как парадокс Гемпеля — второе название она получила в честь немецкого математика Карла Густава Гемпеля, автора её классического варианта. Проблема формулируется довольно просто: каждый ворон имеет чёрный цвет. Из этого следует, что всё, что не чёрного цвета, не может быть вороном. Этот закон называется логическая контрапозиция, то есть если некая посылка «А» имеет следствие «Б», то отрицание «Б» равнозначно отрицанию «А». Если человек видит чёрного ворона, это укрепляет его уверенность, что все вороны имеют чёрный окрас, что вполне логично, однако в соответствии с контрапозицией и принципом индукции, закономерно утверждать, что наблюдение предметов не чёрного цвета (скажем, красных яблок) также доказывает, что все вороны окрашены в чёрный цвет. Иными словами — то, что человек живёт в Санкт-Петербурге доказывает, что он живёт не в Москве.

С точки зрения логики парадокс выглядит безукоризненно, однако он противоречит реальной жизни — красные яблоки никоим образом не могут подтверждать тот факт, что все вороны чёрного цвета.

Источник