К вопросу о сущности денег. IV.1. Двуединство

Является ли экономика точной наукой?

В энциклопедиях и словарях общепризнанная классификация наук отсутствует. Там нет деления наук на точные, гуманитарные, общественные и прочие.

Это правильно. Каждая наука описывает лишь часть нашего целостного мироздания, и, кроме того, науки пересекаются между собой и ветвятся, они взаимопроникновенны.

Общественность обычно называет точными науками физику, химию, астрономию и математику. Я употребил здесь слово «общественность», так как перечень точных наук проскакивает, мелькает чаще всего в публичных выступлениях и общедоступной литературе. Именно проскакивает, а эти четыре науки упоминаются почти во всех «мельканиях». Из этого списка точных наук иногда выпадает химия, а иногда сюда прибавляются финансы, частично биология, информатика и довольно много других дисциплин в зависимости от направления читаемой лекции или публикуемой статьи.

Согласно бытовому толкованию слова, точность есть полное соответствие истине, действительности или образцу – так, по крайней мере, написано в толковых словарях.

Без определения термина «истина» нет и самой точности в её абсолютном понимании.

В более узком смысле можно говорить о точности измерений.

Измерение относится к познавательным процедурам и потому соответствует положениям, принятым в «Теории познания». Один из принципов этой теории гласит, что при конкретизации объекта каждая описывающая его величина может быть измерена, и

нет такой величины, измерение которой не могло бы быть уточнено.

Это означает, что каждая величина имеет диапазон неопределённости, который при измерениях может быть уточнён, сжат, но не ликвидирован. Действительно, если диапазон неопределённости будет сжат до единственного значения, то дальнейшее уточнение при измерении будет невозможно.

Для иллюстрации принципа я привожу стилизованный фрагмент схемы коленвала, понимая, что при единстве мироздания эти рассуждения применимы к любому объекту или явлению вообще, в том числе к экономике.

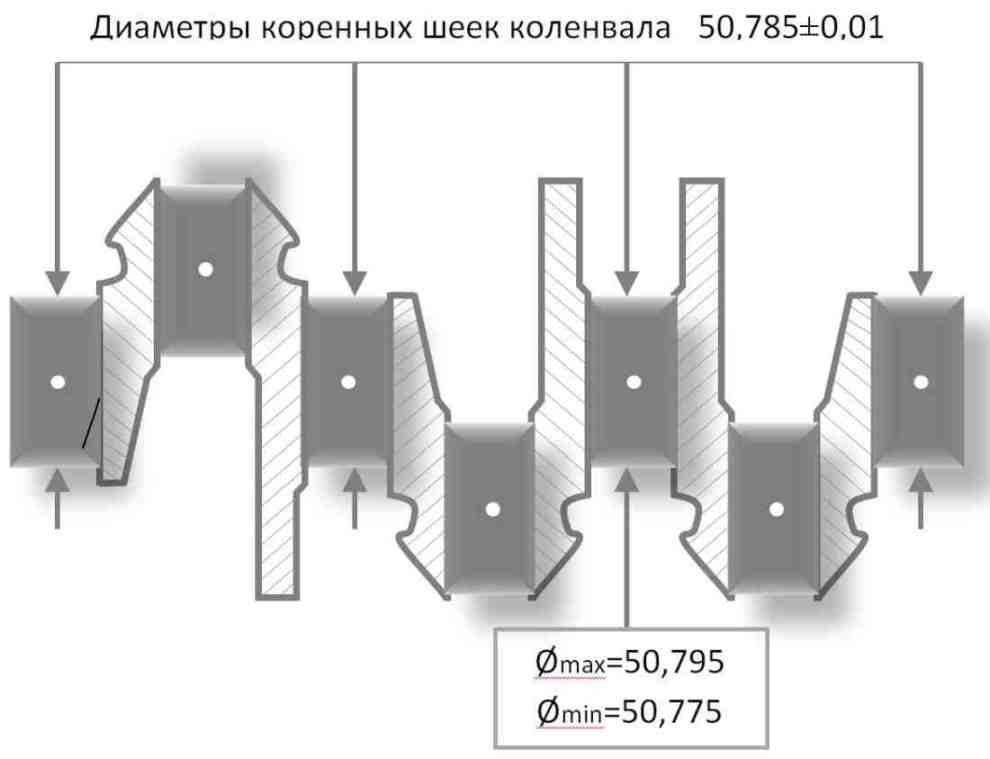
Все изготовленные коренные шейки, диаметр которых уложился в данный диапазон размеров, будут иметь разное числовое выражение диаметра, но все эти диаметры будут истинными величинами для данной модели коленвала (объекта).

Они будут истинными, но всегда разными. Ни одного полного совпадения!

Мы называем эти величины истинными, потому что коленчатые валы с этими, пусть и отличающимися друг от друга, размерами будут выполнять своё предназначение, то есть конкретная модель двигателя с этой деталью будет работать. Если же размер диаметра выйдет за жёстко заданные пределы 50.775÷50.795, то это будет уже другой диаметр, другая величина, характеризующая другой объект, например, металлолом.

Диапазоны возможностей

Во всех рассуждениях я руководствуюсь презумпцией, что каждая величина отвечает принципу двуединства – этому важнейшему принципу мироздания, принципу, согласно которому всё можно рассматривать как композицию табу и случая, действующего в диапазоне, этим табу не охваченном. Я специально взял тут для двуединства эксклюзивные термины, чтобы не касаться давно разрабатываемых философами понятий о случайности и необходимости, о сущности и явлениях, о феноменах и ноуменах, и так далее.

Приведённый на рисунке пример – это иллюстрация принципа двуединства, где границы табу есть минимальный и максимальный размеры 50,785±0,01мм, а диапазоном случайностей являются все значения внутри этих границ. Здесь максимальная абсолютная погрешность оценивается в сотую долю миллиметра, а относительная – примерно в ±0,02%.

Можно, конечно, углубиться в более технологичные сферы, где измерения ведутся в миллионных долях миллиметра и ещё точнее, но и приведённый пример уже воспринимается как прикосновение к точной технической дисциплине. Мы же попробуем двигаться в противоположном направлении и, может быть, нащупаем границу, где научная дисциплина перестаёт восприниматься как точная.

Возьмём, например, ГОСТ 24454-80*, устанавливающий размеры хвойных пиломатериалов. Для обрезной доски толщиной 25мм стандартом устанавливается предельное отклонение ±1,0мм, что соответствует относительной погрешности в ±4,0%. Такая доска мне вполне нравится, и, изготовив из неё опалубку или обрешётку под металлочерепицу, я буду считать изготовителей таких досок людьми аккуратными, владеющими своей специальностью и точно всё рассчитавшими. Соответственно точной мне кажется и наука, рекомендациями которой руководствуются специалисты.

Перейдём от точных наук к научным дисциплинам с большим интуитивным наполнением и посмотрим на очень распространённое в экономических расчётах арифметическое действие – вычисление прибыли:

Прибыль = Выручка – Расходы

Пусть мы израсходовали 95 млн. рублей и получили 100 млн. Наша прибыль составила 100 – 95 = 5 млн. рублей. Это то, что мы хотим получить по чисто формальным признакам (математически). Согласно нашим мечтам, так насчитает бухгалтер, когда дело будет закончено.

Но до конечной бухгалтерии нам ещё очень далеко, и мы хотим прикинуть, в каком интервале может находиться реальная величина прибыли при условии, что нам известна ошибка исходных данных.

Для большей наглядности используем приведённую нами чуть выше «техническую» погрешность исходных данных в ±4%. Тогда:

Расходы = 95±3,8 млн. рублей;

Выручка = 100±4 млн. рублей

Результат = 5±7,8 млн. рублей.

То есть разница между затратами и выручкой может меняться от убытка в 2,8 до навара в 12,8 млн. рублей. Неопределённость возросла с 4% у исходных данных до100×7,8/5 = 156% у результата (желанной прибыли). Точность конечного результата по сравнению с исходными данными упала больше, чем на порядок.

При таком подходе нет нужды обращаться и к методам оценки неопределённости, а если проще, то к методам теории вероятности: мы этим интервалом [−2,8÷12,8 млн. рублей] накрыли все возможные значения ожидаемой прибыли.

Но если мы хотим рискнуть в надежде всё же получить прибыль, то это будет уже азартная игра, потому что у нас всего одна попытка, а не их множество. Нам не надо попадать в интервал −2,8 ÷ 0,0 млн. рублей, иначе мы будем в убытке. Применив вероятностный математический аппарат, мы можем помочь своей интуиции. Мысленно надстроим над интервалом (−2,8 ÷ 12,8) кривую плотности некоторого распределения вероятностей. Пусть распределение будет гауссовским. В нашем примере матожидание равно 5,0 млн. рублей, а среднеквадратичное отклонение зададим сами. Пусть оно равняется 1,6 млн рублей. Тогда вероятность работы на прибыль будет где-то у цифры в 99,7%.

Надо понимать, что применение математического аппарата лишь облегчает интуитивный выбор, но не защищает нас от возможного убытка, так как произошедшая (как-то вдруг) реализация события в интервале −2,8 ÷ 0 млн. рублей (расчётная вероятность попадания в этот интервал равна 0,3%) в мгновение ока превращает эту ничтожную математическую вероятность в 100% действительный убыток.

Точность исходных величин по ГОСТ 24454-80* и по экономическому планированию одна и та же, а ощущение точности результата обратное.

Если мир един, то свойством двуединства должны обладать все величины, параметры и объекты мироздания.

1. Развитие науки в целом. Философ и историк науки Имре Лакатос доказывает, что в силу методологических решений сторонников существующей научной парадигмы её «твёрдое ядро» полагается неопровержимым (табу). Эволюция же парадигмы происходит за счёт творческого видоизменения, разработки вспомогательных гипотез и граничных условий в рамках «защитного пояса» (диапазона).

2. Мозг, порождающий науку, тоже не исключение из этой двуединой композиции. Всемирно известный физиолог Н.П. Бехтерева подчёркивает, что мозг осуществляет мыслительную деятельность системой с жёсткими (обязательными) и гибкими (переменными) звеньями. Именно это обеспечивает и надёжность функционирования системы, и огромные возможности её работы в самых разных условиях.

3. Поведение отдельного человека и государств складывается из стратегической линии и динамически меняющейся тактической составляющей.

4. Да и сама человеческая жизнь подчиняется этому принципу: «Она (жизнь) ведь вся, согласно вашей, пусть и условной, теории, проходит между добром и злом, между Богом и дьяволом» (Солоухин В.А., 2009).

Таким образом, разница между величинами заключается не в том, что одни из них являются точными, а другие нет. Разница в степени неопределённости каждой величины, в размерах диапазона, где правит случай и в значимости отношения этого диапазона к жёстко заданной, неизменяемой части − самости величины. Точность же воспринимается субъективно, это понятие из области искусства.

Если не замыкаться на технологических диапазонах машинерии, а посмотреть на экономическое развитие стран, на историю, на жизнь человека, то впору говорить не о диапазонах неопределённости, а о диапазонах возможностей.

Однако диапазон – это мгновенный срез, а мы живём во времени. Во что превращается диапазон, перемещаемый во времени?

Коридоры сомнений

Из-за двуединой сущности величин всё развивается как композиция из жёстких ограничений и случайностей. Движение, называемое временем, создаёт из ограничений жёсткие стены, а из диапазонов получаются коридоры – коридоры неопределённостей, коридоры сомнений или возможностей, коих для любого объекта мириады. Может быть, «композиция» звучит здесь несколько статично и всё это движение больше похоже на фестиваль, калейдоскоп из океана ограничений и случайностей. Каждое свойство объекта, каждая характеристика, каждая величина – от самой действенной, от параметра, до самой ничтожной, не заметной и в микроскоп, – образует свой коридор, а все вместе, переплетаясь и пронизывая друг друга, вырисовывают феерическую, динамичную картину. Как писал поэт, «Лишь сделаю рукой движенье – и новое в глазах явленье!». Никогда не удастся сделать две абсолютно одинаковые гайки, и никогда, при всех прочих равных условиях, в точности не повторится ни одно историческое событие. Велика бывает роль личностей, оказавшихся по воли случая в критических точках этих коридоров, хотя и эти личности, сумев выбрать оптимальную тропу для движения, не в силах пробить стены и порушить стратегические замыслы Создателя.

Математические формулы дают формальное описание, и использование их на практике возможно только после определения коридоров неопределённости (или возможности), где и будут себя реализовывать реальные параметры.

Жизнь и «коридор», конечно, не очень гладко стыкуются: обижает душу такое сравнение. Другие, дабы не провоцировать клаустрофобию, вместо коридоров берут реки, берут струны. Но реки не дают такую предопределённость характеристик. Представляя себя путешествующим по рекам, всегда несёшь в себе надежду, что можно перехитрить Создателя и в случае чего пойти по берегу, а это недопустимо, так как за жёсткие границы ни человек, ни бездушный параметр без потери своей сущности выйти не могут: не для того их создавали.

«Струны, создающие музыку жизни,» − звучит красиво. Но образ струны не несёт в себе ощущение движения во времени. Струна колеблется в заданном диапазоне, создаёт бесчисленное множество случайных реализаций – всё новых и новых мелодий, но чувства поступательного движения здесь нет, только бесконечное дрожание.

Поэтому и далее будем использовать коридоры неопределённости, коридоры сомнений. Даже коридор возможностей, в отличие от диапазона возможностей, как-то давит, не даёт мечте расправить крылья.

Ещё спросим: «А как же прогресс, наука, эволюция»? Это всё локальные законы, законы внутри заданных Создателем границ. Возьмём, к примеру, коридор со стенами «бытие определяет сознание» и «сознание определяет бытие». Все люди всю свою жизнь двигаются между этими стенами. Сначала они прижимаются к первой стене. Но появится кто-то, и его идеи захватят сознание сородичей. Качнётся тропа ко второй стене коридора – и реализованные идеи, то есть сознание, изменит бытие, и вновь откатятся люди к стене бытия, на практике оценивая новые реалии.

Во многих случаях ширина коридоров случайностей либо огромна, либо тропинка в этом коридоре проложена таким образом, что идущие по ней люди карабкаются по холмам и не могут подойти к стенам, а даже увидев их, не могут понять, что по-настоящему ограничивает их движение. Приходится бороться с барханами, со случайными помехами, не осознавая действительных ограничений – стен коридора.

Случайные помехи, как детские куличики, теремки и песочные замки, создают множество случайных реализаций, за которыми очень трудно определить обязательные (жёсткие) звенья. Часто используемый учёными пример – жернова и засыпка. Материал и форма засыпки могут быть разными. Засыпка трясётся, осыпается, закрывает жернова: жерновов за засыпкой нам не видно.

Ясно одно: в современной экономической науке случайные составляющие изучаемых величин и процессов настолько велики, что жернова, жёсткий скелет всеобщей экономической теории мировой наукой даже толком и не разработан, о чём косвенно говорит сегодняшняя точность, вернее, ужасающая неточность экономических прогнозов.

Всё вышесказанное в полной мере относится и к деньгам. Сущность процесса, заключающаяся в необходимости деления благ между частицами жизни, в своём развитии достигла многого. Она, как хамелеон, меняет коллекции одежд. Она является людям то в виде золота или медных монет, то в виде акций, облигаций и прочих изысков, но, гуляя по коридорам неопределённости, эта суть всегда одна и та же.

 Суть всегда одна и та же: деньги, в какие бы одежды они ни рядились,  дают людям право на соответствующую долю благ. Как бы ни множить эти доли, они не могут превысить единицу (100%). Несправедливое распределение денег (долей) множит армию обездоленных. Всё остальное: ссудный процент, золотой, бумажный или электронный носитель - есть случайность, проходящая волна.

 Именно  сути денег и не хочет видеть современная экономическая наука.

Первоисточник: Виногоров Б.Г. К вопросу о сущности денег, или Грустно, господа, или Книга скорби. -М.: [б.и.], 2017. – 159 с. ISBN 978-5-600-01953-9.