Решение уравнений метадинамики

   Метадинамика: решение уравнений метадинамики - создание устойчивого,справедливого общества

Поговорим о решении уравнений метадинамики. О построении устойчивой, предсказуемой системы, предполагается общества, то есть устойчивого, предсказуемого, справедливого общества. Когда мы выводили уравнение, было замечено, что валовое условие совпадения структур производства и потребления является симметрией и так же генерирует пространство симметрии взаимодействия участников экономики, то есть для того что бы удовлетворить валовое или глобальное условие совпадение структур мы должны потребовать такое же совпадение структур в обмене продуктами в экономике натурального обмена. То есть из соотношения двух структур мы должны вывести свойства целого пространства. Это похоже на то как мы из из знаний ускорения получаем знания о траектории, то есть из дифференциальной формы уравнения получаем интегральные характеристики. Именно это нас будет интересовать в нашем случае.

Допустим у нас есть n участников такой экономики. Казалось бы, глобальное требование совпадения структур должно привести к уравнению (aj,ai)=1 для любых j и i. Однако такое решение приводит к неоднозначности. Так в случае с четырьмя участниками может существовать две "глобальные" симметрии такой системы. Соответственно будет присутствовать такая двойная неопределенность. Что бы осталась одна глобальная симметрия, то есть некое единственное глобальное устройство в рамках этих четырех участников, нужно "порвать" некоторые связи, что бы осталась одна глобальная симметрия и соответственно однозначные законы в такой системе.

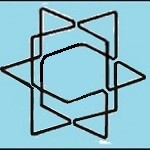
Допустим, что в экономике с n участниками мы оставили только одну глобальную симметрию. То есть, если между двумя участниками в обмене существует симметрия, то там есть линия и все участники соединены между собой одной линией. Понятно, что мы можем расположить всех участников по вершинам многоугольника, так что глобальная симметрия будет соединять участников такой системы по ребрам многоугольника, а диагональные связи будут разорваны. Простой алгоритм: расположение участников по вершинам многоугольникам и разрыв диагональных связей между участниками или вершинами многоугольника, обеспечит нас единственной глобальной симметрией в такой системе.

Если мы будем считать целые связи энергией созидания, а разорванные связи как энергией разрушения, то условием равновесия будет равенство созидания и разрушения, соответственно равенство оставшихся и разорванных связей. Число целых связей равно n, а число разорванных связей равно n*(n-3)/2, приравнивая их получим n=5. То есть единственным многоугольником в котором число разорванных и целых связей равно, является пятиугольник. В четырехугольнике соотношение равно 1/2, а в шестиугольнике 3/2.

Соответственно структуры объектности большей 5 являются неустойчивыми.

Неустойчивость многоугольников можно продемонстрировать построением пространственных структур. Как первый шаг мы буем объединять элементы структуры по 6, потом эти 6 объектные структуры снова объединять еще по 6 штук, затем из этих 6 выделять один и переносить на следующий уровень и повторять эту процедуру. понятно что в зависимости от слоя отношение числа разорванных связей будет соотносится как (3/2)**N где N это номер слоя. То есть относительное число разорванных связей будет расти и соответственно такая структура будет разваливаться.

В случае с четырехугольников соотношение разорванных и целых связей будет расти как (1/2)**N. Относительное число разорванных связей и целых будет уменьшаться с ростом слоев. Структура построенная из четырех объектных структур будет стремиться замкнуться.

В случае пяти объектных структур, соотношение разорванных связей и целых будет сохраняться вне зависимости от номера слоя. Вывод: 1) из пяти объектных структур можно построить устойчивые бесконечные структуры. 2) Пяти объектные структуры являются рекурсивно устойчивыми.

Таким образом наш генератор симметрии свелся к набору всего лишь трех структур, можно сказать симметрий 3го, 4го и 5го порядка. Есть много структур большего порядка, но они неустойчивы. Поэтому если мы будем рассматривать соответствующий вид неустойчивости, обусловленный ростом числа участников структуры, можно ограничится всего лишь одной шести объектной структурой.

В структуре с двумя элементами нет глобальной структуры, поэтому мы ее рассматривать не будем.

Понятно, что если мы будем строить глобальную структуру из пяти объектных структур, то ее энтропия будет на много меньше, чем если бы мы строили систему на единых правилах. Соответственно такой способ построения будет приводить к динамической системе с предсказуемым поведении. В случае социальных систем это называется справедливым общество.

Можно сказать что пяти объектная структура является устойчивой к рекурсии, повторению. Это означает, что мы систему строим по слоям, с уменьшением элементов в каждом слое, и с повторением структуры, то есть в каждом слое структура остается той же самой. Причем такое построение остается устойчивым для пяти объектных структур, в отличии от 4,3,6,7 объектных структур и структур большего порядка. То есть при таком построении возникает дальний порядок, что означает мы можем построить бесконечно большую систему, общество, сознание. Такая система будет единой в смысле минимума энтропии, то есть разногласий и противоречий в этой системе.

Современное общество строится, как правило, на выборах: один президент выбирается для миллионов. Такой способ построения ни в коем случае не снимает никаких противоречий, что и приводит к неоднородности выраженной в эксплуатации, так и неустойчивости выраженной в кризисах и войнах. Но по сути это одно и то же: неоднородность по пространству и неоднородность по времени по сути и есть неустойчивость как в пространстве так и во времени.

И такой способ сведения миллионов в единое порождает неоднородности и не важно это закон в области законодательства, единый президент для общества, единые цены в экономике. Но по сути других правил собственно в современном обществе и нет. Почему они возникли и остаются до нашего времени мы разберем позже.

Популистское:"давайте объединимся и все вместе..." - сделаем то то или другое. Единые правила не означают единое общество, то есть систему соединенную в единое. Единое это минимум разногласий. Просто так собрать всех в одном месте и пойти куда то это далеко не единство, это его видимость, это временная единая цель не более, на мгновение перекрывшая разногласие.

Далекий порядок означает не только пространственную характеристику в этом пространстве, но и так же временную устойчивость, то есть систему с максимальной устойчивостью и размерами как в пространстве так и во времени. Система максимально большая как в пространстве так и во времени.

И такой способ построения возможен как для внешнего так и для внутреннего. Под внутренним тут можно понимать как сознание одного человека, так и устройство небольшого коллектива внутри большого сообщества. Единичный элемент системы устроенная таким образом будет обеспечивать устойчивость и большой размер всей системы.

Энергия это физическая величина и она определяется в физике как собственное число временной симметрии. Мы построили пространство симметрии которое либо слабо, либо никак не связано с нашим физическим пространством. Тем не менее, это пространство симметрии и оно так же имеет энергию, но это не физическая энергия, это, скорее всего, есть та самая тонкая энергия, которая связана с субъектом. Нет симметрии, значит нет тонкой энергии и значит нет субъекта.

Текст полной теории находится тут: mentagen.ru/info/teory Ментаген это сокращенное от "ментальный геном" - система, которая помогает строить отношения в различных областях как область симметрии, как субъектность.

Статистика систем, построенных на пяти объектных структурах, будет совпадать со статистикой пяти объектных структур. Например, статистика сознания, как бы это не звучало парадоксально, так же определяется пяти объектной структурой, но это совпадает с реальными числами. Пяти объектность сознания можно трактовать как наличие пяти не совпадающих стратегий, например: правила поведения в семье различаются от правил поведения среди друзей по увлечению и от правил поведения на работе. Наличие различных, не совпадающих стратегий и дает устойчивость при смене обстановки, при необходимости смены стратегии поведения и эту устойчивость можно посчитать и сравнить с действительностью.