Эта старинная городская игра помогла открыть новый раздел математики!

В средневековом немецком городе Кёнигсберг (современный российский Калининград) на реке Прегель рядом располагались два острова. Берега реки с островами и острова между собой были соединены в общей сложности семью мостами.
Среди местных жителей ходила интересная игра: они пытались пройти по всем семи мостам так, чтобы ни разу не повторить один и тот же. Однако ни у кого это не получалось!
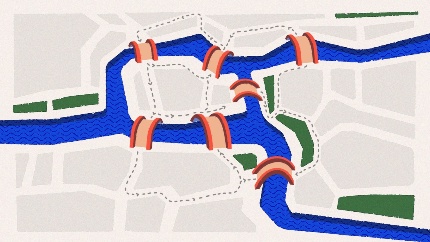
Загадкой заинтересовался петербургский математик и академик Леонард Эйлер. В 1736 году он написал огромный труд, решая эту задачу — и стал отцом целого нового раздела математики, которую позже назвали теорией графов.
Эйлер нарисовал все точки на суше, куда должен попасть человек по мостам, а потом соединил их линиями так, как должен пролегать маршрут. Получилась сложная фигура — граф, то есть множество точек, соединенные линиями «ребрами». «Эйлеровым путем» называется как раз тот путь, который подразумевает прохождение по всем ребрам, ни разу не повторившись.
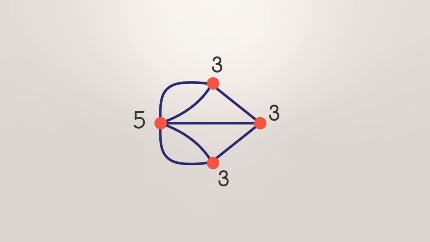
Если вкратце – задачу решить нельзя. Эйлеров путь возможен только если в графе не более двух нечетных вершин (то есть вершин, из которых выходит нечетное количество линий). А здесь их больше двух.
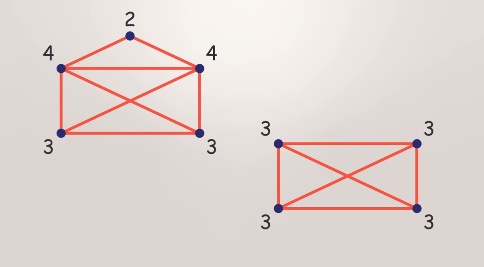
Похожую задачку дают детям: открытый конверт можно нарисовать одним росчерком пера, а вот закрытый - нет. Потому что в открытом – две нечетные вершины (с цифрами 3), а в закрытом аж четыре.
Кстати, вживую проверить решение задачи уже не получится. Ныне из семи мостов сохранились только два: Деревянный и Медовый. Другие были либо перестроены (и соединены в одну эстакаду), либо безвозвратно разрушены во время Великой Отечественной войны.
















Оценили 53 человека
94 кармы