Теория низковисящих плодов или асимптотический тупик.

    В нашем мире есть один универсальный закон, он универсален везде, на всех континентах и во все времена. По-видимому он универсален и для всей деятельности человека.

     Разные люди называют его по разному: одни теорией низковисящих плодов, другие теорией убывающей отдачи от инвестиций, третьи асимптотический тупик, четвертые видят на графике S-образную кривую. 

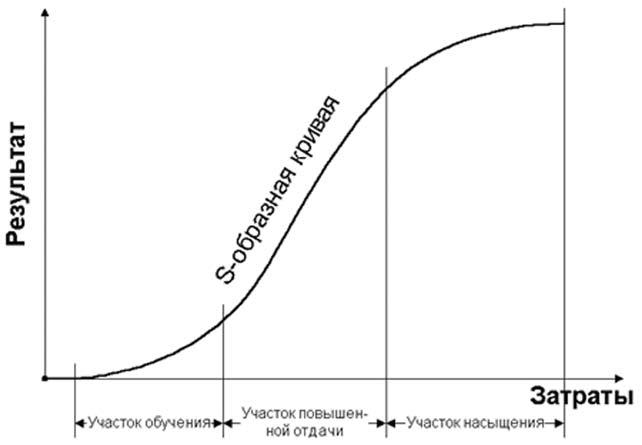
   Эта теория абсолютно противоположна тому, что воспевал Ричард Бах в своем бессмертном произведении "Чайка по имени Джонатан Ливинстон".        

   Ричард Бах был оптимистичен. Он, устами мудрой чайки говорил, что границ познания вселенной и себя нет! 

    И вроде как он прав, ведь вселенная бесконечна, а число вариантов связей между нейронами человека от этой вселенной не отстает.

    Но на практике, если отрешиться от красивостей, границы есть! Они мягкие и поначалу легко поддатливые, и если сначала на кривой внедрения и развития технологии технологии небольшие инвестиции в познание природы позволяет добиться впечатляющих результатов, 

чему примером весь 19 и частично 20 век, то затем наступает технологический предел или  асимптотический тупик. 

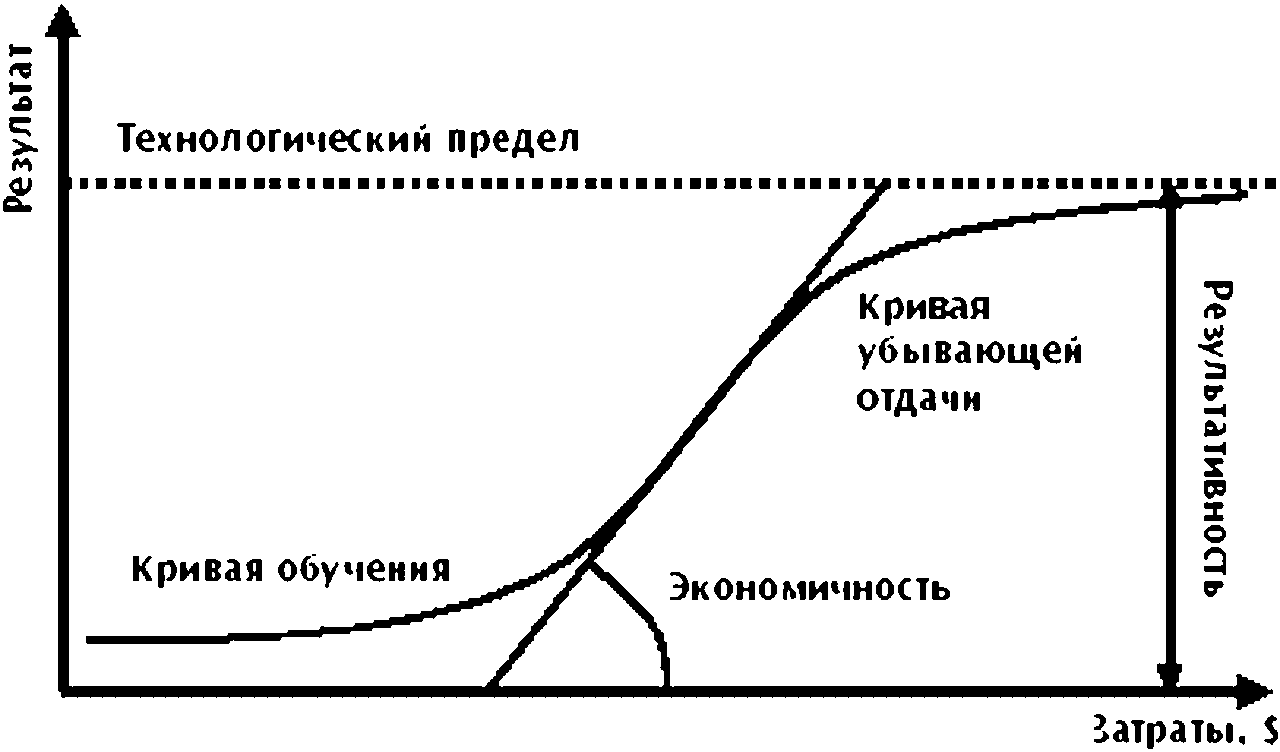
   Это значит, что для того чтобы развиваться дальше, надо прикладывать все больше и больше усилий, а отдачи все меньше и меньше, ведь низковисящие плоды знаний уже в основном все сорваны. 

   Но это одна технология может зайти в тупик, а наша цивилизация держится на огромном множестве технологий и если одна из них приближается к технологическому тупику, как пример технология винтовых самолетов:

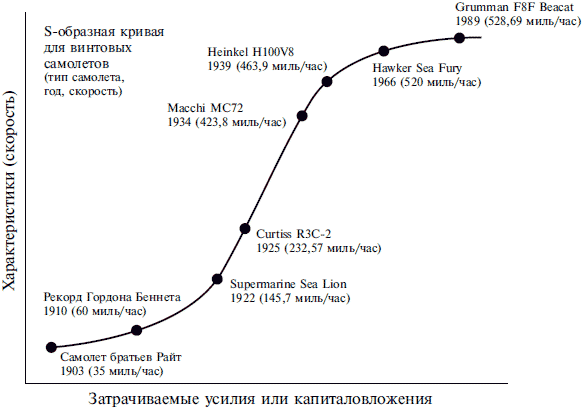
то ее тут же подхватывает другая и график 2-го более высокого уровня выглядит так:

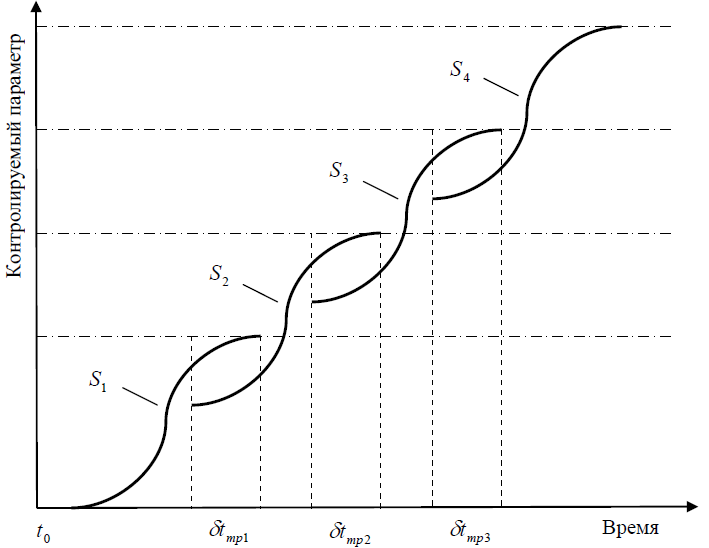
    Кажется, что прогресс не остановим! 

   Но так ли это?

  Дело в том, что по мере прогресса, задачи усложняются. Ещё Пифагор заметил, что знания подобны кругу, чем больше знаешь, тем с бОльшим незнанием граничишь (тем, следовательно, дороже обходится каждый шаг).
- Каждый способен освоить 4 действия арифметики буквально на лету. Простая механика по силам каждому.
- Тригонометрия чуть сложнее, её приходится изучать, тратя на это время (да и то, не каждый выносит из школы то, чему его, вроде бы, обучали). В радиотехнике разбирается не так много человек, да и то не переведутся верующие в то, что из колебательного контура можно извлечь энергию (та же РЕЗОНАНС!).
- Дифференциальное исчисление проходят в школе, но немногие могут сходу указать смысл производной или, хотя бы, продифференциировать функцию по графику; составлять и решать дифференциальные уравнения не могут более 95% населения. Обычная классическая электродинамика 19-го века за пределами понимания этих 95% людей.
- Интегральное исчисление в полной мере - отдельная и сложная наука. Немногие люди с высшим образованием способны взять сложный интеграл и владеют хотя бы элементарным интегрированием по вычетам. Контурные интегралы, интегралы по путям, теория функций комплексных переменных, понимание операционного исчисления и начал линейной алгебры с теорией групп - доступно не более, чем 1% населения. Квантмех и самые простые его следствия - привилегия этих немногих. Простой пример: программировать может каждый, любой но полезных квантовых алгоритмов придумано всего 3 (прописью: три!). Несмотря то, что за новый полезный квантовый алгоритм объявлены многомиллионные премии (не одна, не одна!).
- Та же самая математика, но в полном объёме, на уровне полноправного пользователя доступна максимум одной десятой процента. Даже самые начала дифференциальной геометрии и простейшие операции на многообразиях (кто из местных сможет изложить суть гипотезы геометризации Пуанкаре?) - тайна и мистика для 99.99% людей. Понимание доказательства гипотезы Пуанкаре (в сильном смысле) доступно людям, которых можно перечислить на листе формата А3 некрупным шрифтом. Теория относительности никогда не будет осознана 99.9% людей. КЭД, не говоря уж о КХД, будут понятны (я имею в виду - в полной мере, а не на уровне избранных анекдотов) только спецам, которые потратили от 5 до 7 лет жизни на изучение этих областей знания. В М-теории и суперсимметриях понимают толк тоже только спецы, развивают их единицы.
...и это ещё фигня. Потому что...
- Современная дифференциальная геометрия, современная теория алгоритмов, современная /подставить всё, что угодно/ - доступны людям, которые не просто входят в интеллектуальную элиту человечества, но и избрали для себя в жизни такой путь - работать на науку. Все остальные - стоят в сторонке и курят. Хуже того: эта элита, эти люди могут не иметь понятия (и часто не имеют) о совершенно элементарных вещах из другой области знаний. Мозги человеческие и главное - доступное человеку время (время!) слишком малы, чтобы вместить в себя всё многообразие того, что уже поняло человечество. Люди тратят 7-10 лет только чтобы выйти на передний край науки... а чтобы сделать что-то своё, это необходимо... Хуже всего то, что люди подходят к этому краю уже не в 20-25 лет, как раньше, а в 28-30. Это ещё достаточно плодотворный возраст, хотя и не пик. Но что будет, если экстраполировать то, что мы имеем?
К чему этот мой долгий спич?
К тому, судари и сударыни, что прогресс замедляется по объективным причинам. Крайне маловероятно, что вы сможете придумать новый термоядерный движок, не понимая ничего в физике плазмы. Вы не сможете разработать новые материалы, не зная основ физики твёрдого тела. Даже сугубо инженерные задачи (если мы говорим о прорывах) требуют всё большего от инженеров, знаний, умений но что ещё хуже: интеллекта. Чтобы применять что-то в технике, нужно как минимум это что-то хотя бы немного понимать. 

    Потому, если отойти от нашего графика все дальше и дальше, и дальше и дальше, , то можно увидеть график еще более высокого (3-го) порядка, когда множество S-образных кривых снова сливаются в одну тонкую линию. 

   И что же увидим? Я не могу точно сказать, но мне кажется, что мы увидим нечто вроде этого графика:

     На этот раз окончательного. 

     А если законы физики одинаковы в любом месте вселенной, не в этом ли отгадка "Великого Молчания Космоса"?