Меновые отношения без введения стоимостных отношений и стоимости

Меновые отношения без введения стоимостных отношений и стоимости

Положим [3], что условное общество состоит из трёх агентов производства, которые производят все необходимые продукты для его действительной жизни. При этом каждый агент производства производит лишь один вид продукта, но потребляет продукты всех трёх производимых в этом «обществе» видов. Стадии-шаги цикла воспроизводственного кругооборота (обращения) объектов как элементов, продуктов, действительной жизни показаны на схеме рисунка 1.

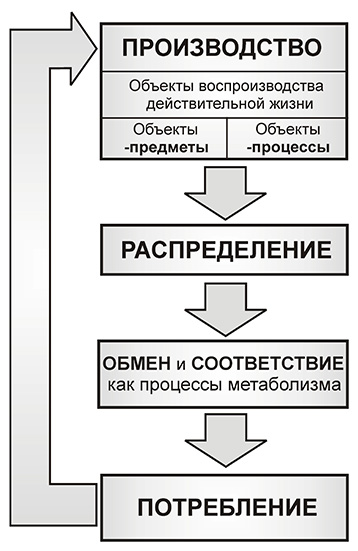
Рис. 1. Стадии цикла воспроизводственного кругооборота (обращения) производства как «общественного движения»

Первый шаг - производство.

Производство продуктов в этом примере в количественном измерении отображено в левой части таблицы рисунка 2 «Производство».

С целью упрощения положим, что каждый агент производит только один вид продукта:

- агента-производитель с индексом i = 1 производит продукт с индексом j = 1 в количестве Pj=1 = 6000 штук;

- агента-производитель с индексом i = 2 производит продукт с индексом j = 2 в количестве Pj=2 = 9000 штук;

- агента-производитель с индексом i = 3 производит продукт с индексом j = 3 в количестве Pj=3 = 12000 штук.

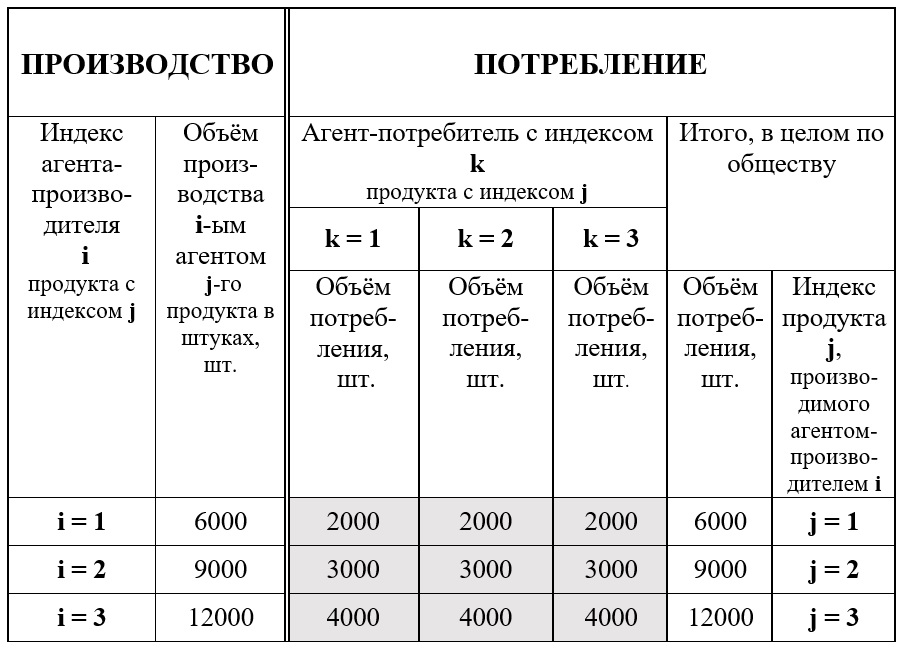
Рис. 2. Балансовая матрица «производство-потребление», описывающая равновесное состояние общества (при условии равенства структур производства и потребления по каждому агенту и равенства между собой самого воспроизводственного потребления этих агентов)

Второй шаг - распределение.

Как ранее было отмечено, - «распределение устанавливает долю каждого индивида в произведенном» [5]. Положим, «доли» каждого из агентов в произведённом соответствуют тому количеству продукта, которое им произведено, то есть равны 1,0.

Тогда в результате распределения первый агент-производитель (индекс i = 1) получает то, что произвёл, то есть 6000 штук продукта с индексом j = 1. Второй агент-производитель (индекс i = 2) получает то, что произвёл, то есть 9000 штук продукта с индексом j = 2. Третий агент-производитель (индекс i = 3) получает то, что произвёл, то есть 12000 штук продукта с индексом j = 3. Это распределение в табличной форме воспроизведено на рисунке 2.

Таким образом i-ые агенты производства являются одновременно и i-ыми агентами-владельцами созданных ими же в производстве j-ых продуктов (см. таблицу рис. 2).

Третий шаг - обмен.

Известно, что, как пишет К. Маркс, - «Производство создает предметы, соответствующие потребностям; распределение распределяет их согласно общественным законам; обмен снова распределяет уже распределенное согласно отдельным потребностям» (Выделено мной. – ХАТ) [5];

Из того же анализа следует, что структура потребления и структура производства идентичны, ибо «производство есть непосредственно также и потребление» [5]. Это тождество структур производства и потребления соответствует равновесному состоянию воспроизводственного процесса действительной жизни общества.

Предположим, что структуры потребления каждого из агентов общественного воспроизводственного процесса равны между собой и равны структуре производства. При этом изначально в цикле этого воспроизводственного кругооборота обращения все агенты являются агентами-производителями, которые затем, с одной стороны, - выступают в качестве агентов-владельцев продуктов, а позже, уже с другой стороны, - выступают на данном шаге «вторичного» распределения через «обмен» уже как агенты-потребители (см. левую часть таблицы рис.2). В данном примере структура производства и структура первого распределения равны между собой и представлены в натуральном выражении, в штуках (см. рис. 2).

Отобразим структуру производства в относительных единицах, имея ввиду, как исходную, натуральную количественную оценку в штуках каждого из производимых и полностью потребляемых j-ых продуктов. Соответствующая пропорция в потреблении каждым агентом-потребителем действительной жизни общества является пропорция, выраженная, например, в целых действительных числах (или в долях).

Для рассматриваемого условного примера имеем следующую структурную пропорцию производства между j-ыми продуктами:

Pj=1 : Pj=1 : Pj=1 = 6000 : 9000 : 12000 = 2 : 3 : 4.

Соответственно, для рассматриваемого условного примера, получим следующую пропорцию потребления в действительных числах между j-ыми продуктами по каждому агенту-потребителю, помня о её равенстве структуре производства:

2 : 3 : 4.

В результате отмеченное выше тождество структур производства и потребления подкрепляется равенством самих численных выражений соответствующих пропорций в действительных числах:

2 : 3 : 4 = 2 : 3 : 4.

Заметим, что каждый агент одновременно выступает как в роли агента-производителя с индексом i, так и в роли агента-потребителя с таким же номером индекса. Общепринято, что при обозначении (индексации) элементов ячеек таблицы первый индекс всегда указывает строку данной матричной таблицы, поэтому сохраним за первым индексом «i» первоначальное обозначение агента-производителя (строка).

Однако, для данного примера, в целях удобства восприятия, вторым, дополнительным, индексом «j» обозначим вид продукта.

Так как агентами-потребителями являются те же агенты-производители, но выступающие в роли агентов-потребителей, то введём для них новый третий индекс «k» (вместо индекса «i»), который соответствует столбцу агента-потребителя в правой части матрицы таблицы рисунка 2.

Тогда количество продукта в каждой ячейке собственно балансовой матрицы, выделенной на рисунке 2 серым тонированием, будет иметь тройное индексирование с индексами «i», «j» и «k», а сам элемент с количеством продукта в штуках будет обозначаться как – pijk (i = 1, 2, …, m; j = 1, 2, …, q; k = 1, 2, …, n). В данном примере максимальные значения индексов «i», «j» и «k» равны, соответственно, m = 3, q = 3 и n = 3.

Описанная индексация полностью соответствует собственно матричной таблице, выделенной тонированием на рисунке 2.

Эта матричная таблица «обменов» производимыми в обществе j-ыми продуктами потребления между i-ыми агентами-производителями и k-ыми агентами-приобретателями для последующего потребления уже как k-ыми агентами-потребителями. Этот «обмен» как элементарная операция общественного метаболизма обеспечивает, с учётом последующего потребления, воспроизводственную жизнедеятельность i-ых агентов данного условного общества и вместе с этим, можно сказать, и само воспроизводство всей действительной жизни этого условного общества.

В качестве примера образного пояснения дадим следующий комментарий по строке агента-производителя продуктов с индексом i = 2, производящего продукт с индексом j = 2 в количестве 9000 штук (средняя строка матричной таблицы). Этот объём производства распределяется (можно сказать, - отчуждается), по 3000 штук между всеми тремя агентами-приобретателями. При этом агент с индексом k = 1 приобретает продукт с индексом j = 2 в объёме 3000 шт., агент с индексом k = 2 приобретает (сам у себя, то есть оставляет себе для собственного потребления, i = k = 2) продукт с индексом j = 2 в количестве 3000 шт. и, наконец, агент с индексом k = 3 приобретает продукт с индексом j = 2 в количестве 3000 шт.

Пока лишь, предварительно, заметим, что фиксируемый в каждой ячейки матрицы объём того или иного продукта, с одной стороны, «отчуждается», а, с другой стороны, - «приобретается».

Четвёртый шаг - потребление.

Давая полную характеристику одного цикла воспроизводственного кругооборота (обращения) для буржуазного общества, точнее, товарного производства и потребления, К. Маркс пишет:

«Производство создает предметы, соответствующие потребностям; распределение распределяет их согласно общественным законам; обмен снова распределяет уже распределенное согласно отдельным потребностям; наконец, в потреблении продукт выпадает из этого общественного движения, становится непосредственно предметом и слугой отдельной потребности и удовлетворяет ее в процессе потребления» (Выделено мной. – ХАТ) [5].

В нашем условном примере предполагается, для упрощения, что объёмы продуктов, приобретаемые путём «обмена» при вторичном распределении для последующего потребления каждым агентом по одноимённым видам продуктов, равны. То есть по каждой тройке индексов i, j и k, относящихся к одной строке матрицы, объёмы потребляемых продуктов pijk равны, равны для каждого агента как приобретателя данного вида продукта.

В то же время структура потребления каждого k-го агента-потребителя, как и было задано, соответствует структуре производства (см. рис. 2).

Так, например, структура потребления агента-потребителя с индексом k=1 (первый столбец собственно балансовой матрицы, выделенной светло-серым тонированием ячеек) в натуральном выражении имеет вид:

p111 : p221 : p331 = 2000 : 3000 : 4000 = 2 : 3 : 4.

Структура производства:

Pj=1 : Pj=1 : Pj=1 = 6000 : 9000 : 12000 = 2 : 3 : 4

Таким образом:

Pj=1 : Pj=1 : Pj=1 = p111 : p221 : p331 = 2 : 3 : 4.

Аналогичные равенства (тождества) имеют место и других агентов-потребителей:

Pj=1 : Pj=1 : Pj=1 = p112 : p222 : p332 = 2 : 3 : 4;

Pj=1 : Pj=1 : Pj=1 = p113 : p223 : p333 = 2 : 3 : 4.

Полученный результат достаточно тривиален и нагляден в отношении чисел, выражающих объёмы продуктов, а путь его получения повторяет четыре шага одного цикла кругооборота (обращения), указанные во введении к «Капиталу» в разделе «2. Общее отношение производства к распределению, обмену, потреблению» [5]. Эти шаги был подробно рассмотрены выше.

Далее.

Рассмотрим собственно саму балансовую матрицу равновесного состояния (см. рис. 3), которая в таблице рисунка 2 выделена серым тонированием, вписав в неё дополнительно по каждому элементу условное обозначение количества продукта, обозначаемое тройной индексацией, - pijk. Тройная индексация непосредственно вводит указание на вид продукта с индексом j (средний индекс), который соответствует рассматриваемому элементу балансовой матрицы с координатами i и k (первый и третий индексы).

Рис. 3. Балансовая матрица «производство - потребление» в условиях равновесного состояния «условного общества»

На рисунке 3 двухсторонними фигурными стрелками соединены те элементы (ячейки) балансовой матрицы, агенты которых, как агенты-производители, вовлечены в «обмен», на что указывает «зеркальное» отображение «крайних» индексов (первого и третьего индексов) этих ячеек, точнее, индексов соответствующих объёмов потребления, то есть - pijk. Это следующие пары объёмов pijk:

p112 = 2000 и p221 = 3000;

p113 = 2000 и p331 = 4000;

p223 = 3000 и p332 = 4000.

Здесь, судя по зеркальному отображение крайних индексов, каждый из агентов выступает одновременно и как агент-производитель (первый индекс тройной индексации - i), отчуждающий свой продукт, и как агент (третий индекс тройной индексации - k), приобретающий для своего потребления продукт другого вида «взамен» отчуждённого им продукта. В результате такого взаимодействия осуществляется метаболический «обменный» процесс, который в буржуазном обществе, в случае, если типологии обеих продуктов «внешний предмет, вещь», принято именовать «товарообменом». Ячейки матрицы рисунка 3 с элементами этих «зеркальных» пар обмена, дополнительно к двухсторонним стрелкам, выделены тонировкой различной интенсивности, но одинаковой для каждой пары.

Так, например, «зеркальная» пара обмениваемых элементов p112 = 2000 и p221 = 3000 соединённых малой двухсторонней фигурной стрелкой и имеющих светло-серое тонирование соответствующих ячеек балансовой матрицы, последовательно читается следующим образом:

- Первый агент с индексом i = 1 отчуждает в пользу второго агента с индексом k = 2 2000 единиц (штук) произведённого им продукта с индексом j = 1, так как согласно матричной таблицы рисунка 2 только этот агент (i = 1) производит продукты с индексом j = 1 (и только этот продукт). При этом другой (второй в этой паре) агент с индексом k = 2 отчуждает в пользу первого агента k = 1 3000 единиц (штук) произведённого им продукта с индексом j = 2, так как согласно матричной таблицы рисунка 2 только этот агент производит продукты с индексом j = 2 (и только этот продукт).

Следующая пара элементов p113 = 2000 и p331 = 4000, соединённых длинной двухсторонней фигурной стрелкой, последовательно читается следующим образом:

- Первый агент с индексом i = 1 отчуждает в пользу третьего агента с индексом k = 3 2000 единиц (штук) произведённого им продукта с индексом j = 1, так как согласно матричной таблицы рисунка 2 только этот агент (i = 1) производит продукты с индексом j = 1 (и только этот продукт). При этом другой (второй в этой паре) агент с индексом i = 3 отчуждает в пользу первого агента k = 1 4000 единиц (штук) произведённого им продукта с индексом j = 3, так как согласно матричной таблицы рисунка 2 только этот агент производит продукты с индексом j = 3 (и только этот продукт).

Наконец, пара элементов p223 = 3000 и p332 = 4000, соединённых малой двухсторонней фигурной стрелкой и имеющих тёмное тонирование соответствующих ячеек балансовой матрицы, последовательно читается следующим образом:

- Агент с индексом i = 2 отчуждает в пользу третьего агента с индексом k = 3 3000 единиц (штук) произведённого им продукта с индексом j = 2, так как согласно матричной таблицы рисунка 2 только этот агент производит продукты с индексом j = 2 (и только этот продукт). При этом другой (второй в этой паре) агент с индексом i = 3 отчуждает в пользу агента с индексом k = 2 4000 единиц (штук) произведённого им продукта с индексом j = 3, так как согласно матричной таблицы рисунка 2 только этот агент производит продукты с индексом j = 3 (и только этот продукт).

Таким образом имеем три «меновых» отношения для всех трёх продуктов производимых и потребляемых в рассматриваемом иллюстративном примере условного общества. Эти три меновых отношения представлены в таблице рисунка 4.

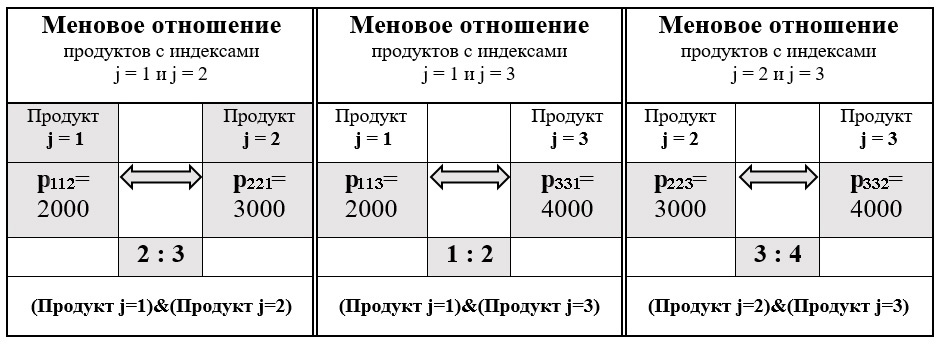
Рис. 4. Меновые отношения для всех трёх продуктов производимых и потребляемых в рассматриваемом иллюстративном примере условного общества

Выполненный анализ условного примера формирования балансовой матрицы «производство – потребление» на основе целостного единства воспроизводственного процесса действительной жизни общества позволил показать, что, так называемое «меновое отношение» возникает не на базе «меновой стоимости товаров», которая «и есть их стоимость» как утверждает автор «Капитала». В частности, К. Маркс пишет:

- «Таким образом, то общее, что выражается в меновом отношении, или меновой стоимости товаров, и есть их стоимость.

… Как же измерять величину ее стоимости? Очевидно, количеством содержащегося в ней труда, этой «созидающей стоимость субстанции». Количество самого труда измеряется его продолжительностью, рабочим временем …» (Выделено мной. – ХАТ) [1, с. 4].

Базой возникновения менового отношения, как показывает приведённый условный пример одного цикла кругооборота (обращения) воспроизводственного процесса, является устойчивое сохранение равновесного состояния общества как единого целого, что «свойственно всякому органическому целому». При этом заметим отсутствие в приведённом анализе даже какого-либо упоминания стоимости, рабочего времени и опосредуемого им «труда, этой «созидающей стоимость субстанции», - по Марксу.

Следовательно, можно полагать, что полученные в условном примере «меновые отношения» есть выражение «органическим целым» общества его целостного единства. А это отторгает утверждение автора «Капитала» о стоимости, лежащей в основе менового отношения, - «пропорции»:

«Меновая стоимость прежде всего представляется в виде количественного соотношения, в виде пропорции, в которой потребительные стоимости одного рода обмениваются на потребительные стоимости другого рода …» [1, с. 2].

Вместе с этим, выявленным нами, отторжением «обессмысливается» и такое заключение:

«Стоимость одного товара относится к стоимости каждого другого товара, как рабочее время, необходимое для производства первого, к рабочему времени, необходимому для производства второго. «Как стоимости, все товары суть лишь определенные количества застывшего рабочего времени»» [1, с. 5].

Наконец, как пишет К. Маркс, - «Если отвлечься от потребительной стоимости товарных тел, то у них остается лишь одно свойство, а именно то, что они – продукты труда» [1, с. 3], - но этим отторгается, скорее, - «ущемляется», само понятие менового отношения, так как не только «продукты труда» охватываются меновым отношением. В отличие от монологического и гомогенного «Капитала» с его монообъектом «внешний предмет» (товар!), в действительной жизни социума меновыми отношениями охватывается множество разнообразных нетоварных, гетерогенных, базовых объектов следующих типологий (см. метатеорию «Полилогия современного мира …» [4]): человек, общая жизнь, работник, пространство производства, средства производства (товар), функции (технологии), информация, общественное познание и др.

Более того, дальнейшие пояснения автора «Капитала» окончательно, и наглядно, демонстрируют нелепость предлагаемой в «Капитале» трактовки понятия «стоимость»:

«Вещи, которые сами по себе не являются товарами, например, совесть, честь и т. д., могут стать продажными для своих владельцев (предметом продажи - ХАТ) и, таким образом при посредстве цены (благодаря своей цене – ХАТ) приобрести товарную форму. Следовательно, вещь формально может иметь цену, не имея стоимости» [1, с. 56].

Так как этот «пассаж» нами неоднократно комментировался, например, в работе «Кризис …» [2], то ограничимся лишь этой ссылкой, однако дополнительно заметим, что во многом этот пассаж продиктован пониманием стоимости как «овеществлённого человеческого труда» и труда как «целенаправленной деятельности».

В заключение следует особо заметить, что выполненный выше анализ формирования балансовых матриц общества в их равновесном состоянии показал возможность его использования в условиях неоднородности и неоднозначности самих количественных оценок различных продуктов и процессов, отображаемых в матрице баланса.

Литература

1. Маркс К. Капитал. Критика политической экономии. Т. 1. Книга 1. Процесс производства капитала. М.-Л.: Государственное издательство, 1929.

2. Харчевников А. Т. Испорченный капитализм: Рыночный фетишизм товаризации – [б. м.]: Издательские решения (По лицензии Ridero), 2020.

3. Харчевников А. Т. Матрица «обменов»: Полилогия метаболизма. [б. м.]: Издательские решения (По лицензии Ridero), 2020.

4. Шушарин А. С. Полилогия современного мира (Критика запущенной социологии). В 5 т. Раздел 2: Эндогенная логика. М.: Мысль, 2005.

5. http://eurasian-defence.ru/sites/default/files/data/201305/kapital.pdf