Космос - одно из самых загадочных понятий в мире. Если ночью посмотреть на небо, можно увидеть несметное количество звёзд. Да, наверное, каждый из нас слышал, что во Вселенной больше звёзд, чем песчинок в Сахаре. И учёные с древних времён тянулись к ночному небу, стараясь разгадать загадки, скрывающиеся за этой чёрной пустотой. Начиная с древних времён они совершенствовали методы измерения космических расстояний и свойств звёздного вещества (температуры, плотности, скорости вращения). В этой статье мы расскажем о том, что такое параллакс звезд и как он применяется в астрономии и астрофизике.
Явление параллакса тесно связано с геометрией, но прежде чем рассмотреть геометрические законы, лежащие в основе этого явления, окунёмся в историю астрономии и разберёмся в том, кто и когда открыл это свойство движения звёзд и первым применил его на практике.

История
Параллакс как явление изменения положения звёзд в зависимости от расположения наблюдателя известно очень давно. Ещё Галилео Галилей писал об этом в далёком Средневековье. Он лишь предполагал, что если бы можно было заметить изменение параллакса для далёких звёзд, это было бы доказательством того, что Земля вращается вокруг Солнца, а не наоборот. И это было сущей правдой. Однако доказать это Галилео не смог из-за недостаточной чувствительности тогдашней аппаратуры.
Ближе к нашим дням, в 1837 году, Василий Яковлевич Струве провёл серию экспериментов по измерению годичного параллакса для звезды Веги, входящей в созвездие Лира. Позже эти измерения признали недостоверными, когда в следующем после публикации Струве году, 1838-м, Фридрих Вильгельм Бессель измерил годичный параллакс для звезды 61 Лебедя. Поэтому, как бы это ни было печально, приоритет открытия годичного параллакса принадлежит всё-таки Бесселю.
Сегодня параллакс используется как основной метод измерения расстояний до звёзд и при достаточно точной измерительной аппаратуре даёт результаты с минимальной погрешностью.
Нам следует перейти к геометрии перед непосредственным рассмотрением того, что такое метод параллакса. И для начала вспомним самые азы этой интересной, хотя и нелюбимой многими науки.
Основы геометрии
Итак, то, что нам необходимо знать из геометрии для понимания явления параллакса, - это то, как связаны значения углов между сторонами треугольника и их длины.
Начнём с того, что представим себе треугольник. В нём есть три соединяющихся прямых и три угла. И для каждого разного треугольника - свои величины углов и длин сторон. Нельзя изменить размер одной или двух сторон треугольника при неизменных значениях углов между ними, это одна из фундаментальных истин геометрии.
Представим, что перед нами стоит задача узнать значение длин двух сторон, если мы знаем только длину основания и величины углов, прилегающих к нему. Это возможно с помощью одной математической формулы, связывающей значения длин сторон и величин углов, лежащих напротив них. Итак, представим, что у нас есть три вершины (можете взять карандаш и нарисовать их), образующие треугольник: A, B, C. Они образуют три стороны: AB, BC, CA. Напротив каждой из них лежит по углу: угол BCA напротив AB, угол BAC напротив BC, угол ABC напротив CA.
Формула, которая связывает все эти шесть величин вместе, выглядит так:
AB / sin(BCA) = BC / sin(BAC) = CA / sin(ABC).
Как мы видим, всё не совсем просто. У нас откуда-то появился синус углов. Но как нам найти этот синус? Об этом мы расскажем ниже.

Основы тригонометрии
Синус является тригонометрической функцией, определяющей координату Y угла, построенного на координатной плоскости. Чтобы показать это наглядно, обычно чертят координатную плоскость с двумя осями - OX и OY - и отмечают на каждой из них точки 1 и -1. Эти точки расположены на одинаковом расстоянии от центра плоскости, поэтому через них можно провести окружность. Итак, мы получили так называемую единичную окружность. Теперь построим какой-нибудь отрезок с началом в начале координат и концом на какой-нибудь точке нашей окружности. Конец отрезка, который лежит на окружности, имеет определённые координаты на осях OX и OY. И значения этих координат и будут представлять собой соответственно косинус и синус.
Мы выяснили, что такое синус и как его можно найти. Но на самом деле этот способ чисто графический и создан скорее, чтобы понять саму суть того, что представляют собой тригонометрические функции. Он может быть эффективен для углов, не имеющих бесконечных рациональных значений косинуса и синуса. Для последних же более эффективен другой метод, который основа на применении производных и биномиального вычисления. Он носит название ряда Тейлора. Рассматривать этот способ мы не будем потому, как он достаточно сложен для вычисления в уме. Ведь быстрые вычисления - это работа для компьютеров, которые созданы для этого. Ряд Тейлора используется в калькуляторах для вычисления многих функций, включая синус, косинус, логарифм и так далее.

Всё это довольно интересно и затягивающе, но нам пора двигаться дальше и вернуться к тому, на чём мы закончили: на задаче по вычислению значений неизвестных сторон треугольника.

Стороны треугольника
Итак, вернёмся к нашей задаче: нам известны два угла и сторона треугольника, к которой эти углы прилежат. Нам нужно узнать всего лишь один угол и две стороны. Самым лёгким представляется нахождение угла: ведь сумма всех трёх углов треугольника равна 180 градусам, а значит, можно легко найти третий угол, вычтя из 180 градусов значения двух известных углов. А зная значения всех трёх углов и одной из сторон, можно найти длины двух других сторон. Вы можете проверить это самостоятельно на примере любого из треугольников.
А теперь наконец поговорим о параллаксе как о способе измерения расстояния между звёздами.

Параллакс
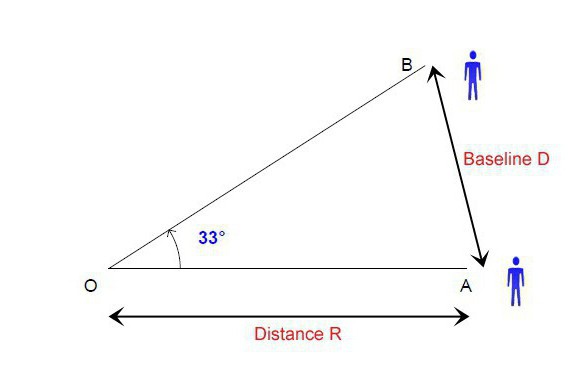
Это, как мы уже выяснили, один из самых простых и действенных методов измерения межзвёздных расстояний. Параллакс основан на изменении положения звезды в зависимости от расстояния до неё. Например, измерив угол видимого положения звезды в одной точке орбиты, а затем в прямо ей противоположной, мы получим треугольник, в котором известна длина одной стороны (расстояние между противоположными точками орбиты) и два угла. Отсюда мы сможем найти две оставшиеся стороны, каждая из которых равна расстоянию от звезды до нашей планеты в разных точках её орбиты. В этом и заключается метод, с помощью которого можно вычислить параллакс звезд. Да и не только звезд. Параллакс, эффект которого оказывается на деле очень простым, несмотря на это, используется во многих своих вариациях в совершенно разных областях.
В следующих разделах рассмотрим подробнее области применения параллакса.

Космос
Мы говорили об этом не раз, ведь параллакс - это исключительное изобретение астрономов, призванное измерять расстояния до звезд и прочих космических объектов. Однако тут не всё так однозначно. Ведь параллакс - это метод, у которого есть свои вариации. Например, различают суточный, годичный и вековой параллаксы. Можно догадаться, что все они различаются промежутком времени, которое проходит между этапами измерений. Нельзя сказать, что увеличение временного промежутка увеличивает точность измерения, потому как цели у каждого вида этого метода свои, а точность измерений зависит лишь от чувствительности аппаратуры и выбранного расстояния.
Суточный параллакс
Суточный параллакс, расстояние с помощью которого определяется с помощью угла между прямыми, идущими к звезде из двух разных точек: центра Земли и выбранной точки на Земле. Так как мы знаем радиус нашей планеты, не составит особого труда, используя угловой параллакс, вычислить расстояние до звезды, пользуясь описанными нами ранее математическим методом. В основном суточным параллаксом пользуются для измерения недалёких объектов, таких как планеты, карликовые планеты или астероиды. Для более больших используют следующий метод.

Годичный параллакс
Годичный параллакс - это всё тот же метод измерения расстояний с той лишь разницей, что он сфокусирован на измерение расстояний до звёзд. Это как раз тот случай параллакса, что мы рассматривали в примере выше. Параллакс, определение расстояния до звезды с помощью которого может быть довольно точным, должен обладать одной важной чертой: расстояние, с которого измеряется параллакс, должно быть чем больше, тем лучше. Годичный параллакс удовлетворяет этому условию: ведь между крайними точками орбиты расстояние достаточно велико.
Параллакс, примеры методов которого мы рассмотрели, безусловно, представляет собой важную часть астрономии и служит незаменимым инструментом в измерении расстояний до звёзд. Но на деле сегодня пользуются лишь годичным параллаксом, так как суточный может заменить более продвинутая и быстрая эхолокация.
Идём дальше. Параллакс - это всё-таки оптическое явление, и было бы странно, если бы его свойства использовали лишь в астрономии. Есть ещё одна область применения этого эффекта.
Фотография
Пожалуй, самым известным видом фотографического параллакса можно считать бинокулярный параллакс. Вы его наверняка замечали и сами. Если поднести к глазам палец и по очереди закрывать каждый глаз, можно заметить, что угол зрения на объект меняется. То же самое происходит и при съёмке близких объектов. В объектив мы видим изображение под одним углом зрения, но на самом деле фотография получится с немного другим углом, так как есть разница в расстоянии между объективом и видоискателем (отверстием, через которое мы смотрим, чтобы сделать фотографию).
Перед тем как мы закончим эту статью - пара слов о том, чем же может быть полезно такое явление, как оптический параллакс, и почему стоит узнать о нём больше.
Почему это интересно?
Для начала, параллакс - это уникальное физическое явление, позволяющее нам без особого труда узнать многое об окружающем нас мире и даже о том, что находится за сотни световых лет от него: ведь с помощью этого явления можно вычислять и размеры звёзд.
Как мы уже убедились, параллакс не такое уж далёкое от нас явление, он окружает нас везде, и с помощью него мы видим так, как есть. Это, безусловно, интересно и захватывающе, и именно поэтому стоит обратить внимание на метод параллакса, хотя бы из любопытства. Знание никогда не бывает лишним.
Заключение
Итак, мы разобрали, в чём заключается суть параллакса, почему для определения расстояния до звёзд необязательно иметь сложную аппаратуру, а лишь телескоп и знание геометрии, как это применяется в нашем организме и почему нам может быть это так важно в повседневной жизни. Надеемся, представленная информация была вам полезна!













Оценили 28 человек
35 кармы