"И все-таки она вертится!"
Г. Галилей / Д. Баретти
Данный материал представляет собой ответ на статью alexandr44 "ПЕРЕПОЛЮСОВКА. Экстренный выпуск. К сожалению, не праздничный". (https://cont.ws/@sahalara/1549...)
Немного теории
Момент инерции - интегральная характеристика твердого тела, используемая при описании его вращательного движения. Момент инерции тела относительно некоторой оси вращения есть сумма произведений масс элементарных объемов (материальных точек) тела на квадрат их расстояний до этой оси. То есть если разбить тело на очень большое число частей, определить для каждой из них произведение ее массы на квадрат расстояния до оси вращения и эти произведения сложить, то получится число, называемое моментом инерции. Если устремить число частей, на которые разбивается тело, к бесконечности, то сумма преобразуется в интеграл. Поэтому формула для определения момента инерции содержит интеграл. Ось вращения, относительно которой ищется момент инерции может быть ориентирована относительно тела как угодно и проходить в любом месте тела (и вне него тоже). Если ось вращения проходит через центр масс тела, то момент инерции называется центральным.
Момент инерции необходим для определения момента количества движения (момента импульса), который является той величиной, которая сохраняется при вращательном движении при отсутствии действующих на тело моментов (первый закон Ньютона). При поступательном движении сохраняется импульс (произведение массы на скорость). Момент количества движения есть произведение момента инерции на угловую скорость. Изменение импульса и момента количества движения определяет то, как будет двигаться тело при действии на него сил и моментов.
Так как мы пользуемся трехмерным представлением пространства, то для описания движения в нем используются три взаимно перпендикулярных оси (три направления). Система координат, построенная на них, называется прямоугольной (декартовой). Тогда, для того чтобы понять, как вращается тело, нужно определить его угловую скорость вокруг каждой из осей системы координат (x, y и z). Эти три величины образуют вектор угловой скорости тела. И наоборот, зная, как направлен вектор угловой скорости и ее величину, можно определить эти три проекции.
Моменты инерции, вычисляемые так, как написано выше, называются осевыми моментами инерции. Следовательно, для описания вращения тела в трехмерной системе координат необходимо знать три осевых момента инерции. Кроме них вводятся центробежные моменты инерции, которые можно назвать перекрестными. При вычислении этих моментов определяется сумма произведений массы элементарного объема тела на расстояние до одной оси и на расстояние до другой оси. Для трехмерной системы координат таких центробежных моментов три. Формулы для моментов инерции можно найти в той же Википедии (Момент инерции).
Таким образом, для тела определяются шесть моментов инерции - три осевых и три центробежных. Эти моменты инерции образуют матрицу, которую называют тензором инерции. На ее главной диагонали находятся осевые моменты инерции, выше и ниже нее - центробежные моменты инерции. При этом матрица является симметричной относительно главной диагонали.
Как было сказано выше, момент количества движения есть произведение момента инерции на угловую скорость. Поэтому, чтобы определить момент количества движения для каждой из осей системы координат (всего их три), необходимо найти произведение матрицы моментов инерции на вектор угловой скорости.
Если два центробежных момента инерции, определенные для одной из трех выбранных осей, равны нулю, то данная ось является главной осью инерции. Осевой момент инерции, определенный для этой оси, называется главным. Если главная ось инерции проходит через центр масс тела, то она называется главной центральной осью инерции, а момент инерции - главным центральным моментом инерции. Следовательно, для любой точки тела можно найти три главные оси инерции и три главные момента инерции, а для центра масс - три главные центральные оси инерции и три главные центральные момента инерции.
Если в качестве осей прямоугольной системы координат выбрать главные оси инерции, то это приведет к тому, что в тензоре инерции (матрице моментов инерции) все элементы, кроме диагональных, будут равны нулю. На главной диагонали будут находиться главные (осевые) моменты инерции. Для такого случая и составил Эйлер уравнения вращательного движения твердого тела, которые теперь называются его именем.
Фокус еще заключается в том, что, зная ориентацию главных осей инерции относительно тела и величины главных моментов инерции, можно найти осевые и центробежные моменты инерции для любых осей. Поэтому главные моменты инерции являются основными характеристиками тела для описания вращательного движения. Три главных момента инерции образуют так называемый эллипсоид инерции. И, теоретически, одному и тому же эллипсоиду инерции могут соответствовать разные, по своей форме и распределению массы, тела.
Пусть теперь тело вращается вокруг одной из осей. Насколько устойчивым будет это вращение? Понятие устойчивости обычно иллюстрируют классическим примером шарика, находящегося на вогнутой, выпуклой и плоской поверхностях. Как же определяется устойчивость движения тела? Пусть на тело подействовали возмущения, которые привели к тому, что тело отклонилось от своего первоначального движения, и это отклонение является малым. Если после прекращения действия возмущений отклонение так и остается малым (т.е. оно на растет), то движение называется устойчивым. Если отклонение стремится к нулю (т.е. тело возвращается к своему первоначальному движению), то - асимптотически устойчивым. Поэтому устойчивость определяют еще как способность тела (объекта) возвращаться к состоянию, которое оно имело до воздействия на него внешних сил и моментов, после прекращения их действия. Если отклонение растет, то движение неустойчивое.
Судят об устойчивости движения тела по уравнениям, которые описывают его движение. И для вращательного движениями ими являются уравнения Эйлера. Итак, выше мы задали вращение вокруг одной из осей и будем считать, что внешние моменты мало влияют на эту угловую скорость. Каким будет такое движение, если главные моменты инерции тела различны? Т.е. оно характеризуется "малым", "средним" и "большим" главными моментами инерции: J1, J2, J3. Согласно уравнениям Эйлера движение вокруг "малой" и "большой" осей вращение является устойчивым, а вокруг оси, для которой главный момент инерции имеет "среднее" значение, - неустойчивым.
Это означает, что если тело вращается вокруг "малой" или "большой" осей, то воздействие внешних моментов приводит только к таким явлениям как прецессия и нутация. А если тело вращается вокруг "средней" оси, то - к "кувыркам Джанибекова" (Пример 5 ниже). Точнее, в идеальном случае - когда на тело не действуют никакие моменты - тело "спокойно" вращается и вокруг "средней" оси. Но если есть хоть какое-нибудь воздействие (для Земли это притяжение со стороны Луны, или удар метеорита), то начинается неуклонный рост отклонения от первоначальной ориентации. Если вспомнить гайку (можно волчок с аналогичными моментами инерции), то это выражается в изменении угла ее наклона относительно линии движения (для волчка это угол отклонения от вертикальной оси). В этом и заключается "кувырок".
Здесь стоит отметить, что периодические "кувырки" правильно называть автоколебаниями, которые также могут быть устойчивыми и неустойчивыми. В нашем случае "кувырки"-автоколебания будут устойчивыми, и для них можно определить амплитуду и период.
Сценарии "кувырка" при вращении вокруг "средней" оси зависят от того, каково приложенное внешнее воздействие. ("Гайка Джанибекова" закручена вокруг "средней оси").
Вариант первый. Воздействие таково, что оно приводит только к появлению угловой скорости по другой оси. Главные оси "гайки Джанибекова" не идеально соосны шпильке, на которую она навинчена. Поэтому при сходе со шпильки у гайки есть как угловая скорость вокруг "средней" оси, так и вокруг другой. В этом случае имеет место гладкое изменение угла отклонения гайки от линии движения (тоже самое демонстрируется, например, на видео с теннисной ракеткой). Скорость отклонения нарастает, достигает максимума, затем уменьшается до нуля, и тело занимает "обратное" положение. Далее все повторяется. Здесь необходимо отметить, что период "кувырков" зависит от разницы между "средним" и "малым", либо "большим", моментами инерции. Чем она меньше, тем больше их период ("кувырки" реже). В принципе, период можно рассчитать, но сейчас не об этом.
График кувырка выглядит так: прямая линия, переход на противоположный по знаку уровень, прямая линия, переход на противоположный по знаку (предыдущий) уровень и т.д. Длительность перехода по отношению к длине прямой линии (на самом деле, если масштабировать этот участок, она не совсем прямая, но на большом масштабе этого не заметно) зависит от соотношения моментов инерции.
Вариант второй. Воздействие приложено так (удар по оси), что после него тело начинает раскачиваться, и постепенно ось, раскачиваясь, отклоняется от первоначального положения, амплитуда раскачки достигает максимального значения, скорость перехода в новое (симметричное) положение становится максимальной. Далее, после приближения к "обратному" положению, амплитуда раскачки начинает уменьшаться до минимума. После прохождения своего минимума амплитуда начинает увеличиваться, и начинается переход, с раскачиванием, к "прямому" положению. Т.е. это тот же самый первый вариант, но сопровождающийся раскачиванием оси.
Имеющие возможность, воспользовавшись уравнениями Эйлера, могут сами смоделировать эти варианты.
Немного про центробежные силы
Как известно, при вращении возникают центробежные силы. Классический пример: раскручивание на веревке ведра, заполненного водой. Что будет происходить с веществом, находящимся на поверхности вращающегося тела?
Представим себе Землю как идеальный шар, и что из одного из вулканов вытекает лава. В начальный момент времени, когда лава находилась на краю жерла, ее линейная скорость в пространстве (если отбросить движение Земли по орбите) равна скорости той точки Земли, где мы поместим наш вулкан - произведению угловой скорости вращения Земли, радиуса Земли и косинуса широты. Относительно поверхности Земли лава была неподвижна. На кусок лавы будет действовать сила притяжения, она направлена в центр Земли, перпендикулярно плоскости горизонта в той точке, где находится вулкан, и центробежная сила, ее угол по отношению к плоскости горизонта равен 90 градусов минус широта (на полюсе центробежная сила действует вдоль горизонта, на экваторе направлена вертикально), а также сила Кориолиса (когда появится скорость относительно поверхности Земли).
Для Земли центробежная сила по своей величине заметно меньше силы притяжения, поэтому отрыва лавы от поверхности наблюдаться не будет (если только лава не вышвыривается с космической скоростью, а мы предположили, что лава все же истекает). Следовательно, ее движение будет определяться только величиной проекции центробежной силы на плоскость горизонта, эта величина определяется синусом широты (на полюсе центробежная сила проецируется на плоскость горизонта целиком, синус равен единице, на экваторе проекция равна нулю, так как синус нуля есть нуль), и силой Кориолиса.
Для упрощения картины пусть высота вулкана будет равна нулю. Если мы сперва смоделируем движение куска лавы по поверхности нашего шара, когда никакого трения не существует, то увидим следующую картину. Кусок лавы, разогнавшись под действием проекции центробежной силы, достигнет экватора, где его скорость по широте будет максимальна, и доберется до той же широты в противоположном полушарии, где скорость по широте будет равна нулю, далее все повторится. График изменения широты будет напоминать синусоиду. Если "включить" теперь вязкое трение, то мы увидим колебательный процесс, который по широте закончится на экваторе (где, вспомним, проекция центробежной силы вдоль горизонта равна нулю). Скорость куска лавы относительно поверхности также станет равна нулю. Если трение сделать побольше, то в другое полушарие кусок лавы перескакивать не будет.
Таким образом, вращение тела приводит к тому, что центробежная сила стремится "собрать" все вещество на экваторе. В пределе мы получим тонкий-тонкий блин. Естественно, этого не происходит, потому что вещество уже находящееся на экваторе противодействует тому, которое стремится на него попасть с высоких широт, да и сила сухого трения не даст добраться до экватора. Но шарик из-за вращения все же приплющивает. Ну, а то вещество, что вращается над поверхностью шара, в блин таки превратится (обратим взоры, например, на газовые гиганты Юпитер и Сатурн).
Немного примеров
С учетом вышесказанного можно рассмотреть следующие варианты распределения массы тела и, следовательно, значений моментов инерции. В этих примерах к центральному осесимметричному телу добавлены дополнительные тела, в результате чего получаются разные варианты соотношений трех главных (осевых) моментов инерции.
Пример 1
Имеется основное тело - шар - и два дополнительных шара, расположенных на противоположных сторонах, которые соединены с главным шаром тонкими перемычками.
Моменты инерции тела:
Jх=1,0205; Jy=2,0628; Jz=2,0628

При расчете моментов инерции здесь и ниже принято, что момент инерции главного шара равен 1.
Пример 2
Малые шары подрезаны, в результате получились плоские поверхности, параллельные плоскости xОy.
Моменты инерции тела (по типу "гайки Джанибекова"):
Jх=1,0078; Jy=1,5691; Jz=1,5744
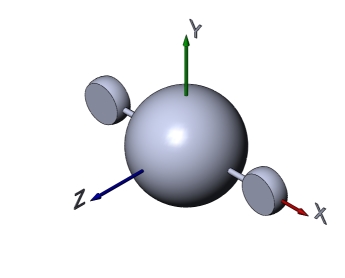
Вращение вокруг "средней" оси y неустойчиво и сопровождается "кувырками".
Пример 3
Малые шары подрезаны, в результате получились плоские поверхности, параллельные плоскости xОz.
Моменты инерции тела:
Jх=1,0078; Jy=1,5744; Jz=1,5691
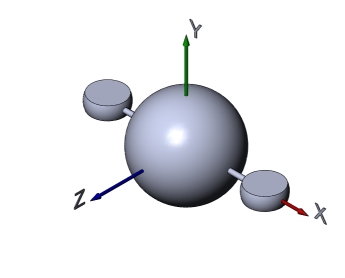
Пример 4
У главного шара имеется тонкое кольцо, расположенное в плоскости xОz.
Сплюснутый шар (эллипсоид) можно представить как шар, к которому добавлено тело, дополняющее шар до эллипсоида. Экваториальное утолщение планеты можно представить в виде кольца.
Моменты инерции тела:
Jх=1,8610; Jy=2,7212; Jz=1,8610
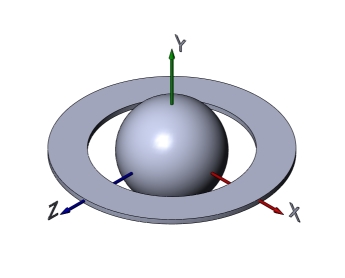
Пример 5
У главного шара имеется тонкое кольцо, расположенное в плоскости xОz, и дополнительные малые подрезанные шары с плоскими поверхностями, параллельными плоскости xОy.
Моменты инерции тела:
Jх=1,6823; Jy=2,9175; Jz=2,2489

Известно, что прецессия и нутация Земли вызвана притяжением, в первую очередь, Луны. Влияют также Солнце и остальные планеты. Это стабильный процесс, он соответствует вращению вокруг "большой" оси (ось y в Примере 4). Увеличение точности описания нутации Земли, например, было осуществлено во второй половине 90-х годов прошлого века (Нутация неупругой Земли (В.Е. Жаров)).
Если период "кувырков" достаточно большой, то за прошедший период астрономических наблюдений современными инструментами, видимо, нельзя сказать, уменьшается ли или увеличивается амплитуда нутации, чтобы можно было говорить о предстоящем "кувырке", если бы Земля вращалась вокруг "средней" оси. На данный момент нет предпосылок к тому, чтобы говорить о "кувырке" на основании наблюдений за нутацией.
Но смена (инверсия) магнитных полюсов по исследованиям палеоархеологов происходила. Да и модель гидродинамического динамо, которым представляют магнитное поле Земли, говорит о том, что магнитное поле переполюсовывается. Правда, с таким большим периодом, что человечество (ну, можно сказать "цивилизованное человечество", это примерно 10 тысяч лет) ни разу эту смену полюсов не испытывало. Да и сама смена "растянута" на 1000 лет, или больше.
В своей статье alexandr44 привел рисунок (https://cont.ws/uploads/pic/20...), который соответствует Примерам 1, 2 и 3. В зависимости от плотности "выступов" соотношение моментов может быть различным, так как момент инерции это интегральная характеристика, и нужно учитывать распределение массы по всему объему. Но скорее всего, если вспомнить про экваториальное утолщение, оно соответствует Примеру 5, следовательно, это "некувыркоспособный" вариант.
Немного фантазии
Силовые линии магнитного поля представляют собой набор тороидов с разными диаметрами сечения (https://upload.wikimedia.org/w..., левый рисунок). И можно, например, представить себе следующую картину. Там, где плотность магнитных линий мала - в приэкваториальной области сферы, - возможно формирование областей с характеристиками, отличающимися от основной массы расплава. Так как вращение связано с гармониками и волнами, то возможно образование в расплаве стоячих волн, которые и приводят к наличию выделенных областей с отличающимися характеристиками (вспоминаем рисунок с "выступами" из статьи alexandr44).
Но можно привести и такой пример с "ушами" (он также понадобится ниже).
Пример 6
У главного шара имеется тонкое кольцо, расположенное в плоскости xОz, между шаром и кольцом имеются дополнительные малые подрезанные шары с плоскими поверхностями, параллельными плоскости xОy. Дополнительные шары не соединены с шаром и кольцом жесткими перемычками. Тело вращается вокруг оси y.
Моменты инерции всего тела равны:
Jх=2,1990; Jy=3,5893; Jz=2,3955
Моменты инерции дополнительных подрезанных шаров:
Jх=0,002566; Jy=0,19767; Jz=0,19899
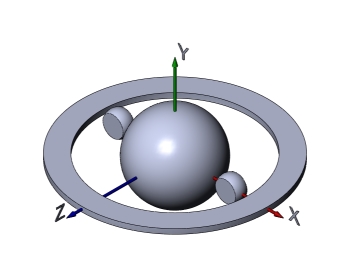
Как было сказано выше, магнитное поле Земли объясняется концепцией динамо. По модели гидродинамического динамо в ее внешнем ядре находится расплавленный электропроводящий слой. Вышеприведенный пример тела может продемонстрировать смену магнитных полюсов, если предположить, что моменты инерции электропроводящего слоя земного динамо таковы, что он вращается вокруг "средней" оси.
Малые подрезанные шары служат имитаторами электропроводящего слоя, точнее, электрических токов в нем. Безусловно, движение в этом слое сложнее, чем то, которое можно описать движением тела, составленного из двух малых шаров (я не берусь моделировать уравнения в частных производных и все, что связано с гидродинамическим динамо). И если этот электропроводящий слой вращается вокруг "средней" оси, то магнитному полю будут присущи "кувырки". В Примере 6 малые шары вращаются вокруг "средней" оси, это вращение "кувыркоспособно".
Возмущения, которые запускают "кувырки" и которые определяют движение магнитных полюсов в данный момент времени, - это излучение Солнца, движение центра масс Земли, гравитационное притяжение объектов Солнечной системы и т.д.
Есть мнение, что смена магнитных полюсов может быть не совсем периодической. Такое может быть. Если на нелинейную систему воздействовать периодическим воздействием, то она может совершать движение, которое по форме будет периодическим, но период будет непостоянным и казаться случайным. Такие квазипериодические, кажущиеся случайными движения в нелинейной системе называют динамическим хаосом (существует достаточное количество примеров его демонстрирующих, например, вращение колеса водяной мельницы). В биологии динамикохаотическое движение характерно, например, для ионных каналов клетки.
Если параметры модели гидродинамического динамо таковы, что в нем возможен динамический хаос, то смены полюсов будут не совсем периодичны. А значит, и движения магнитных полюсов, предшествующие их смене, также будут казаться немного сумбурными, но вполне рассчитываемыми и модулируемыми, и происходить по второму сценарию "кувырка".
Дело в том, что внешние воздействия на Землю из-за ее вращения периодические. И реакция Земли также будет периодической, возможно, с несколькими гармониками. Поэтому будут имеет место раскачивания.
В качестве заключения
Я считаю, что Земле "кувырки" не грозят. Вращение Земли стабильно. Сильно измениться вращение Земли может только в случае жуткого удара метеоритом (какая сила для этого нужна, можно найти, если погуглить по "прецессия и нутация Земли" и т.п. запросам, касающимся вращения Земли).
История Земли это не "кувыркающаяся" история, а история катастрофического, уникального изменения, в которое может входить и инверсия магнитного поля. Или даже, если пофантазировать, его появления. (Познакомиться с описанием одной из теорий-гипотез катастрофического изменения Земли можно, например, в книге В.Н. Ларина "Наша Земля (происхождение, состав, строение и развитие изначально гидридной Земли)", которую упоминает и alexandr44).








Оценили 3 человека
4 кармы