Открытие уравнений гравитации. Загадки.

Часть 1.

    Данную тему следовало создать в 2015 как раз в столетие открытий уравнений гравитации. Но на тот момент у меня не было стройной картины этой запутанной и местами детективной истории. Нет её и сейчас. Тем не менее попытаюсь исторически воспроизвести цепочку событий и возможно кое-какие моменты проявятся более явственно. О том, как были открыты уравнения, которые носят название Гильберта – Эйнштейна (иногда без первой фамилии), были посвещены многие работы в 90-х и начале 2000-х. Но часто они перегружены математическими формулами, в которых простой смертный не в силах разобраться без серьезной подготовки. Я решил все мнения собрать в одном месте.

Опуская достаточно большой промежуток времени, когда Альберт Эйнштейн (А.Э.) был в тяжелом поиске новой теории гравитации, кратко остановлюсь том периоде, когда он вместе со своим институтским товарищем Марселем Гроссманом фактически оформили здание теории, основанной на совершенно революционных принципах и постулатах и затем перейду сразу в 1915 год . (Подробно можно ознакомиться с данным периодом в книге Пайса [1], и статьям В. Визгина [2,3]). Революционная идея состояла в том, что гравитация теперь рассматривалась не как физическое поле, подобно электромагнитному при фиксированной геометрии, а как сама геометрия, только уже не Евклидова и не псевдо Евклидова, а Риманова (точнее псевдориманова). Эйнштейн предложил приравнять тензор энергии импульса вещества 2-го ранга (куда входят все поля, кроме гравитационного) соответствующему тензору, взятому из геометрии Римана с точностью до коэффициента. В этом ему помог Марсель Гроссман. За основу был взят самый простой тензор Риччи и изначально уравнения (с точность до знака) выглядели так:

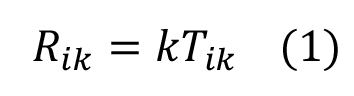
Я предполагаю, что Гроссман был в некотором недоумении от такой идеи, но решил пойти навстречу своему другу, при этом он отвечал только за математическую часть, сняв с себя ответственность за физическую интерпретацию. Именно Гроссман познакомил Эйнштейна с Римановой геометрией. Как видно, если сравнить уравнения на момент 1915 года с правильными, то не хватает еще одного члена: либо 

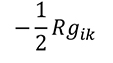
 в левой части, 

либо в правой следового (умноженного на коэффициент k) 

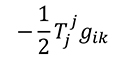
   Но в первоначальном виде уравнения (1) хотя и были ковариантные (то есть модель поля не зависела от выбора системы координат), имели тот недостаток, что ученым не удавалось получить предельный переход в слабых полях в нерелятивистском случае к Ньютоновской теории (не сводились к уравнению Пуассона). Кроме того, не удавалось ввести тензор энергии импульса самого гравитационного поля и возникал псевдотензор. Поэтому Эйнштейну и Гроссману пришлось рассматривать только линейные преобразования координат, а Эйнштейну хотелось получить общековариантные уравнения, например, рассматривать также переход к ускоренным систем отсчета. (Подробнее переход к ньютоновскому потенциалу можно посмотреть у Ландау-Лифшица параграф 99). Далее в ноябрьских статьях А.Э. приходилось ограничивать рассмотрение состояния вещества случаем, когда след равен нулю T=0, что вело также и к ограничению в системе координат и накладывало ограничение на определитель метрики. Эйнштейн считал, что получил нековариантную теорию и это его не устраивало. Дотошный историк этого вопроса и эйнштейновед В.Визгин [2] отмечает, насколько близко находились оба ученых от правильного решения и удивляется, как они не додумались до него.

В поисках союзников Эйнштейн едет летом (июль-август) 1915 в Гёттинген, где сложилась мощная математическая школа во главе с Давидом Гильбертом, Феликсом Клейном и другими ( до этого там работали Герман Минковский и чуть позже Эмми Нётер). Там он читает несколько лекций, излагая свои новые идеи на гравитацию. Там же он сдружился с Гильбертом и у них сложились весьма доверительные отношения.

Эйнштейн Зоммерфельду: «Гильберт меня совершенно очаровал. Выдающийся человек!".

Гильберт Шварцшильду: «гёттингенские лекции Эйнштейна были событием... Астрономы, я думаю, должны сейчас оставьте все остальное в стороне и только попробовать проверить или опровергнуть закон тяготения Эйнштейна!»

Гильберт заинтересовался данной задачей. У него была идея фикс: все явления природы формализовать и аксиоматизировать и данная проблема Эйнштейна в этом контексте выглядела заманчиво – свести гравитацию к геометрии!

Далее Эйнштейн уехал в Берлин, и только в октябре-ноябре снова начинает активно искать решение уже в одиночку. В результате в течение одного месяца он делает Прусскому Королевскому обществу 4 доклада. Никогда ни до ни после он не работал с такой интенсивностью. И уже 25 ноября (в печати 2 декабря) получает верные уравнения интуитивным способом, которые на сегодняшний момент активно проверяются. Фактически можно сказать, что он догадался, что надо добавить к правой части следовой член и записать уравнения в виде:

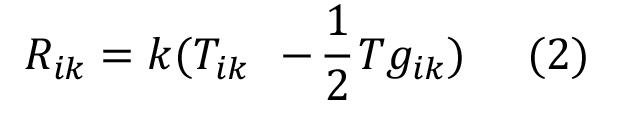
Одновременно в Гёттингене к тем же уравнениям, записанными по-другому, правда в сочетании с электродинамикой Ми, приходит Гильберт, но уже более формально и строго с помощью принципа наименьшего действия. Преимущество вариационного принципа в том, что он сразу дает уравнения в ковариантном виде.

Загадочным оставалось только то, что оба ученых пришли к тем же уравнениям практически одновременно: Эйнштейн 25 ноября, а Гильберт 20 ноября, то есть чуть-чуть раньше. Это было странновато, но не так чтобы совсем невозможно. Таким образом, до начала 80-х годов в научном мире сложилось мнение, что оба великих ученых построили теорию гравитации одновременно.

Все было бы хорошо, но в конце 70-х обнаружилась переписка между Гильбертом и Эйнштейном и оказалось, что они находились в тесном эпистолярном контакте, что могло повлиять на ход их мыслей при построении теории. Историки отмечали тогда, что если бы немецкая почта работала не столь педантично (фактически они получали письма на следующий день после отправки), то вопрос приоритета открытий уравнений сложился бы в пользу Гильберта.

На российско-германском фронте в это время воцарилось затишье. И в это же время Давид Гильберт организует конференцию по своей новой теории и назначает дату коллоквиума в Гёттингене на 16 ноября, а 20 уже делает полноценный доклад Королевскому обществу Гёттингена. Вот переписка того периода с переводом из статьи А.А.Логунов-М.А. Мествиришвили-В.Н. Петров [4].

Геттинген, 13 ноября 1915 г. Гильберт — Эйнштейну

”Собственно я хотел лишь дать приемлемое для физиков изложение связи между физическими константами прежде, чем давать мое аксиоматическое решение Ваших великих проблем. Но если Вы так заинтересованы, то я мог бы в следующий вторник, послезавтра (т.е. 16) изложить мою теорию во всех деталях. Я нахожу ее математически идеально красивой, хотя расчеты не вполне прозрачны, и, строго говоря, не соответствуют аксиоматическому методу. Вследствие одной общей математической теоремы электродинамические уравнения (в основном максвелловы) являются математическими следствиями уравнений гравитации, так что гравитация и электродинамика фактически неразделимы….

• Прошу Вас приехать, хотя бы только на вторник. Вы можете приехать сюда к 3 или 6 1/2. Заседание Математического общества происходит в 6 часов в конференц-зале. Моя жена и я будем очень рады, если Вы разместитесь у нас. Будет еще лучше, если Вы приедете уже в понедельник, так как в понедельник в 6 часов мы проводим в Физическом институте физический коллоквиум. С наилучшими пожеланиями и в надежде на то, что скоро увидимся. Насколько я понимаю Вашу новую работу, Ваше решение совершенно отличается от моего, тем более, что у меня es должны также с необходимостью содержать электрический потенциал”.

Берлин, 15 ноября 1915 г. Эйнштейн — Гильберту

”Ваше исследование меня очень интересует, тем более, что я часто ломал голову над тем, чтобы перебросить мост между гравитацией и электромагнетизмом. Замечания, которые Вы делаете в Ваших письмах, дают основания ожидать чего-то великого. Однако я должен сейчас отказаться от поездки в Геттинген и набраться терпения до той поры, пока смогу изучить Вашу систему из напечатанной работы; я очень переутомился и, сверх того, измучен болями в желудке. Пошлите мне, пожалуйста, если можно, экземпляр корректуры Вашего исследования, дабы удовлетворить мое нетерпение. С наилучшими пожеланиями и сердечной благодарностью Вам и Вашей супруге".

Комментарий: Альберт Эйнштейн хотя и ссылается на недомогание, на самом деле активно работает и заканчивает статью со сложными вычислениями сдвига перигелия Меркурия, исходя из своей теории. Поскольку на 20 назначен доклад Гильберта по своей новой теории, как считает Tilman Sauer, он был обязан отправить тезисы своего доклада всем участникам. Так или иначе (по дружбе), он отправил письмо с тезисами доклада Эйнштейну или целиком доклад. Это письмо, к сожалению, утеряно, иначе бы дальнейших вопросов и последующей интриги не возникли бы. Обратно Гильберт получает ответ.

Берлин, 18 ноября 1915 г. Эйнштейн — Гильберту

"Система, приведенная Вами, точно согласуется, насколько я могу видеть, с тем, что я получил в течение последних недель и направил в Академию (выделено нами — А.А.Л., М.А.М., В.А.П [4].). Трудность состоит не в том, чтобы найти общековариантные уравнения для g„: это легко получается с помощью тензора Римана. Действительно же трудно было понять, что эти уравнения дают простое и естественное обобщение закона Ньютона. Это впервые мне удалось сделать в последние недели (я посылал Вам мое первое сообщение), тогда как единственно возможные общековариантные уравнения, которые теперь оказываются правильными, мы рассматривали уже 3 года назад вместе с моим другом Гроссманом. Только с тяжелым сердцем отказались мы тогда от них, так как физические соображения в пользу их несовместимости с законом Ньютона показались мне тогда убедительными. Самое главное, что эта трудность теперь преодолена. Я сегодня направляю в Академию работу, в которой, исходя из общей теории относительности и без дополнительных гипотез, получил количественно открытое Леверье смещение перигелия Меркурия. До сих пор это не удавалось ни одной теории гравитации. Желаю Вам всего наилучшего".

Комментарий: Хотя Эйнштейн пишет, что получил правильные уравнения, в трех статьях он не упоминает об этом. В статьях 4, 11, 18 ноября нет правильных уравнений со следовым членом. Зато 18 ноября А.Э. лично делает доклад Королевскому обществу в Берлине, видимо, чтобы застолбить приоритет и совершенно не ссылается на Гильберта. При этом он сильно спешит и делает много технических ошибок вплоть до того, что в конце расчетов неправильно делает приближение в подынтегральном выражении и неправильно его интегрирует. При этом, что удивительно, получает правильный ответ: вековой сдвиг перигелия Меркурия 43”. Он по-прежнему стоит на позициях, что состояние вещества должно быть с нулевым следом и ограничивает рассмотрение случаем, когда определитель метрики равен 1. (Подробнее 17 технических опечаток и ошибок рассмотрено в статье [7]). И только 25 ноября в докладе он дает уже правильные уравнения (в печати доклад появился 2 декабря). И выписывает уравнения в виде (2).

Давид Гильберт расстроен. Ему кажется, что Эйнштейн несправедливо забрал у него правильные уравнения и хочет присвоить себе лавры теории. Он пишет в ответ с долей сарказма:

Геттинген, 19 ноября 1915 г. Гильберт — Эйнштейну

(В переводе В. Визгина [3]) . "...Сердечнейшее поздравление по поводу решения проблемы движения Меркурия. Если бы я мог считать так же быстро, как Вы, то электрон должен был бы капитулировать перед лицом моих уравнений, а атом водорода принес бы свои извинения за то, что не излучает...".

В свою очередь обиделся и сам Альберт Эйнштейн. 26 ноября он пишет Цандеру письмо, смысл которого в том, что теория получилась невероятной красоты, но только один человек её понял и он хочет её себе присвоить. Обиду Эйнштейна можно понять. Ведь это он сформулировал идею и мучительно долго оформлял её математически, чтобы не было противоречий.

Уже через месяц, когда страсти немного улеглись, он пишет Гильберту 20 декабря 1915 г. примирительное письмо, в котором витиевато призывает снова к дружбе. Дальнейшая переписка между ними не найдена.

Берлин, 20 декабря 1915 г. Эйнштейн — Гильберту

"Между нами было известное расстройство отношений (eine gewisse Verstimmung), причины которого я не хочу анализировать. Я боролся с чувством горечи, вызванным этим, и притом с полным успехом. Я снова думаю о Вас с безмятежной приветливостью (ungetrьbter Freundlichkeit) и прошу Вас думать обо мне так же. Действительно жаль, когда два настоящих парня (zwei wirkliche Kerle), которые как-то вырвались из этого жалкого мира, не доставляют друг другу радости". (в переводе В. Визгина [3]).

Метод Гильберта состоял в том, чтобы выписать Лагранжиан в самом простом виде: 

R√(-g) , чтобы удовлетворить условиям Эйнштейна – уравнения должны содержать вторые производные линейным образом и члены высших порядков производных отсутствуют. Условие весьма странное, но на сегодняшний день является доминирующим. Вариация по n метрическим функциям в пространстве ранга 4, где возможна симметрия при любых преобразованиях четырёх координат, как выяснилось, дает n-4 независимых уравнений. Это обстоятельство обнаружил Гильберт, получив тождества Бианки.

Альберт Эйнштейн шел, как мы видим, к правильной цели витиеватым и интуитивным путем, постепенно отказываясь от ограничений на координатные преобразования. Очень может быть, что потерянное в архивах Эйнштейна письмо от 14-15 ноября содержало уже правильные уравнения, но со скаляром R в левой части. Это его и натолкнуло на то, чтобы заменить тензор Риччи на тензор другой тензор (Эйнштейна), хотя это было не так очевидно. Или просто, на идею добавить половинный следовой член в правую, и тогда условие на T=0 становилось необязательным. Таким образом, роль Гильберта в вопросе получения уравнений гравитации сильно выросла.

Но это не конец истории. Дотошный В. Визгин [2] отмечал в книге 1981, что Гильберт ссылается на доклад Эйнштейна от 25 ноября, хотя сдал статью в печать 20-го. Далее начинаются еще более странные и детективные события.

(продолжение следует).

Часть 2.

    Понимая какую-то незаконченность в этой истории и в попытках отвергнуть обвинения Эйнштейна (в который раз) в плагиате, группа израильских ученых в 1996 году отправляются в Гёттинген, чтобы восстановить хронику событий и найти новые исторические факты. Они таки их находят. Оказывается, пока статья находилась в издательстве, а процедура публикации дело не быстрое (она появилась в печати 31 марта 1916) , Гильберт 6 декабря сделал ряд исправлений и корректив. Эта дата и стоит на новой редакции статьи. Во-первых, он сослался на доклад А. Эйнштейна от 25 ноября. Во-вторых, ряд положений было переписано и дополнено. И главное – в старой редакции не оказалось выражения со следовым членом. Разбору этих дополнений посвящены работы:

Corry L, Renn J, Stachel J "Belated decision in the Hilbert ë Einstein priority dispute" Science 278 1270 (1997) и В.Н. Визгина [3]. Джон Стейчел – последовательный защитник работ Эйнштейна сразу зацепился за новые исторические открытия.

Но эти господа-ученые идут дальше. Они не только подвергают сомнения приоритет Гильберта, но и его самого обвиняют в том, что именно он позаимствовал правильные уравнения у Эйнштейна. Странно, что к этой позиции присоединились сам Владимир Визгин и некто Алексей Левин - обозреватель интернет-журнала Elementy.ru , который в обзоре к 100-летию открытий уравнений гравитации выделяет в основном роль Альберта Эйнштейна.

http://elementy.ru/novosti_nauki/432628/Stoletie_OTO_ili_Yubiley_Pervoy_noyabrskoy_revolyutsii/t1763182/Aleksey_Levin

Поэтому у читателей и поклонников «Элементов» могло сложиться неверное представление о реальном положении дел с открытием уравнений в 1915 году. В чем прав (и то частично) А. Левин, это в том, что можно вывести значение векового сдвига перигелия Меркурия не имея точных уравнений, а только вакуумных: Тензор Риччи равен нулю. Тогда решая уравнения в фиксированной координатной системе, при условии сферической симметрии и при граничных условиях на бесконечности, можно найти решение данной задачи. Хотя даже здесь Шварцшильд пишет письмо Эйнштейну о неоднозначном решении.

По всем этим «аргументам», что типа Гильберт не нашел точных уравнений, танком прошелся академик А.А. Логунов с коллегами [4] в статье «Как были открыты уравнения Гильберта-Эйнштейна» от 2004 года. Кроме серьезной математической разборки статей Гильберта и Эйнштейна, авторы отмечают, что в обнаруженном оригинальном докладе содержится лакуна: небольшой участок статьи был варварски отрезан и исчез. На этот момент обратил внимание также и F. Winterberg [6]

https://www.researchgate.net/publication/276345765_On_Belated_Decision_in_the_Hilbert-Einstein_Priority_Dispute_published_by_L_Corry_J_Renn_and_J_Stachel

Именно там в отрезанном куске по их мнению и были Гильбертом выписаны уравнения со следовым членом. Вот этот оттиск. 

Страница 8 и 11:

Страница 7:

Видно на 11 странице, что Гильберт ссылается на уравнение (17), которого нет в уцелевшей части. И далее страница (7) отрезана прям по строчке. Поэтому мысль, высказанная рядом исследователей, что это сделал сам Гильберт, маловероятна. Вот, что пишет Винтерберг:

«Осматривая оборотную сторону страницы 8, которой является страница 7, можно заметить, что срез не является прямым, а немного скошенным, перечеркивающим предложение на 7-й странице. Это наводит на мысль, что данный срез был сделан не аккуратно ножницами, а небрежно лезвием бритвы или перочинным ножом, которым воспользовались в особом собрании читального зала Геттингенской библиотеки с целью удалить доказательство того, что Гильберт имел правильную заключительную формулу полевого уравнения раньше Эйнштейна. Приоритет Гильберта поддерживается многими физиками, включая знаменитого физика Стивена Хокинга. Как заметил Х. A. Бьёркнес , данный характер среза указывает на то, что злоумышленник отрезал страницу 8, а не 7, поддерживая, таким образом, версию, что именно Гильберт списал у Эйнштейна, а не наоборот.»

Винтерберг стоит на позициях, что ОТО разработали три человека: Гроссман, Эйнштейн и Гильберт.

Логунов считает, что название уравнений должно содержать две фамилии: Гильберт и Эйнштейн.

Странную двойственную позицию занял еще один новоиспеченный эйнштейновед - Ханс Оханьян, который считает, что в тот момент ни один из участников не создал законченной теории гравитации. Гильберт пытался соединить гравитацию с электродинамикой Ми, последняя потом как научное течение не состоялась. В этом смысле Тензор вещества справа у Эйнштейна был более универсальным.

Для меня осталось не до конца ясным, зачем Давид Гильберт правил свой доклад. Ни Логунов, ни Визгин не дают четкого ответа. Видимо он понял, что не все складно в теории и уравнениях. Получив тождества Бианки, было понятно, что в полной системе не хватает 4 –х уравнений. Гильберт решает их дополнить уравнениями законов сохранения из теории Ми и теория становилась нековариантной. Уже потом стало понятно, что решения ищутся с точностью до 4-х произвольных преобразований координат. Но поскольку Эйнштейн в письме от 18 ноября пишет, что уравнения Гильберта в точности согласуются с его, то странно слушать утверждения, что он их не получил раньше Эйнштейна.

В дальнейшем Давид Гильберт практически не участвовал в развитии теории, но в 1927 году он пишет «Основания физики (второе сообщение)», где ещё раз дает следствия теории и анализирует весьма сложную систему уравнений. Он, как серьезный математик, очень хорошо понял то, что потом многие не могли понять. Выяснилось, что в ОТО нельзя сформулировать закон сохранения энергии гравитационного поля, поскольку вместо тензора энергии-импульса возникал псевдотензор. Затем, он уделил некоторое время постановки задачи Коши и понял, что из-за того, что уравнения неполны, теорема Коши об однозначном решении не работает, а задача с начальными данными зависит от добавочных координатных условий. Также, чтобы в теории не возникало замкнутых времениподобных (и вселенных типа Гёделя), Гильберт добавил некоторые неравенства, ограничив решения физическими метриками и обеспечив тем самым принцип причинности. Эти неравенства есть в ряде учебников по ОТО, но в ряде случаев от них отказываются.

Таким образом, можно сделать вывод, что не все просто в вопросе приоритета открытий уравнений гравитации, и отрицать или принижать роль кого либо из участников было бы неправильно.

1.Пайс А Научная деятельность и жизнь Альберта Эйнштейна (М.: Наука, 1989) с. 5 [Pais A "Subtle is the Lord...": The Science and the Life of Albert Einstein (Oxford: Oxford Univ. Press, 1982)]

2. Визгин В. П. Релятивистская теория тяготения {истоки и формирование. 1900-1915 гг.) (М.: Наука, 1981)

3. Визгин В.П. Об открытии уравнений гравитационного поля Эйнштейном и Гильбертом (новые материалы) . УФН, 2001, том 171, номер 12, страницы 1347–1363 (Mi ufn1962)

4. Логунов А А, Мествиришвили М А, Петров В А "Как были открыты уравнения Гильберта-Эйнштейна?" УФН 174 663–678 (2004)

A.A. Logunov, M.A. Mestvirishvili, V.A. Petrov Russian State Research Center "Institute for High Energy Physics", 142281 Protvino, Moscow Region, Russian Federation

5. Corry L, Renn J, Stachel J "Belated decision in the Hilbert ë Einstein priority dispute" Science 278 1270 (1997) Renn J, Stachel J, Preprint No. 118 (Berlin: Max-Planck Institut fur Wissenschaftsgeschichte, 1999)

6. F. Winterberg. «On “Belated Decision in the Hilbert-Einstein Priority Dispute”, published by L. Corry, J. Renn, and J. Stachel.» 2004. https://www.researchgate.net/publication/276345765_On_Belated_Decision_in_the_Hilbert-Einstein_Priority_Dispute_published_by_L_Corry_J_Renn_and_J_Stachel

7. Anatoli Andrei Vankov General Relativity Problem of Mercury’s  Perihelion Advance Revisited. https://arxiv.org/pdf/1008.1811.pdf