Физики поставили новый рекорд в квантовой суперпозиции.

В.К. В сети появилась вот такая интересная информация:

                              Фото: Yaakov Fein, Universität Wien

Две тысячи атомов впервые поместили в состояние суперпозиции, в котором они пробыли 7 миллисекунд.

Принцип квантовой суперпозиции был протестирован в совершенно новом масштабе. В новом исследовании учёных из Венского университета (в сотрудничестве с Базельским университетом) сложные молекулы, состоящие из почти двух тысяч атомов, были приведены в квантовую суперпозицию, где были доступны для вмешательства. Достижение суперпозиции в новом массовом масштабе установило новые улучшенные ограничения на альтернативные теории в квантовой механике.

Эксперимент продемонстрировал возможность квантового вмешательства во всё более массивные объекты. Используемые молекулы имели массу, превышающую 25 000 единиц атомной массы, что в несколько раз превышает массу объектов предыдущих экспериментов. Одна из самых больших молекул, посылаемых через интерферометр (C707H260F908N16S53Zn4), состоит более чем из 40000 протонов, нейтронов и электронов с длиной волны де Бройля в тысячу раз меньше диаметра даже одного атома водорода. Учёные использовали специальные методы для синтеза таких массивных молекул, чтобы те были достаточно стабильны для образования молекулярного пучка в сверхвысоком вакууме. Молекулы находились в состоянии суперпозиции более 7 миллисекунд, что достаточно долго, чтобы установить новые интерферометрические границы для альтернативных квантовых моделей. Авторы работы уверены, что будущие эксперименты добьются применения квантовой механики в ещё более массовом масштабе.

Источник: https://naukatv.ru/news/25958

Наряду с этой информацией, появилась и ещё не менее интересная информация:

 Трёхщелевой эксперимент.

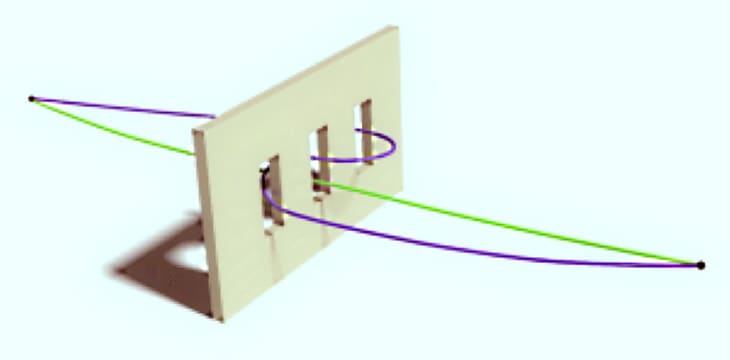
      Пример «неклассической» траектории (фиолетового цвета) в эксперименте с тремя щелями. R. Sawant et al., / PRL

Международная группа физиков экспериментально подтвердила, что при прохождении фотона через три щели вклад в получаемую в результате интерференционную картину дают и невозможные с точки зрения классической физики траектории. Это открытие подтвердило некорректность широко распространенного наивного понимания принципа квантовой суперпозиции и, возможно, позволит усилить существующие схемы работы квантовых компьютеров. Работа опубликована в журнале Nature Communications. С ее текстом можно ознакомиться также на сайте препринтов arxiv.org.

Группа экспериментаторов, возглавляемая известным физиком Робертом Бойдом (который, в частности, был первым, кто осуществил «замедление света» при комнатной температуре), придумала и реализовала схему, демонстрирующую вклад так называемых «неклассических» траекторий в картину, получаемую при интерференции фотонов на трех щелях.

Интерференция на двух щелях — это классический эксперимент, демонстрирующий волновые свойства света. Впервые он был осуществлен в самом начале XIX века Томасом Юнгом и стал одной из главных причин отказа от доминирующей тогда корпускулярной теории света.

В начале XX века, однако, было выяснено, что свет все же состоит из частиц, получивших название фотонов, но эти частицы загадочным образом обладают и волновыми свойствами. Возникла концепция корпускулярно-волнового дуализма, которая была распространена также и на частицы материи. В частности, наличие волновых свойств было обнаружено у электронов, а позднее и у атомов и молекул.

В квантовой механике — новом разделе физики, возникшем в результате этих открытий, — возникновение интерферометрической картины в эксперименте с двумя щелями играет одну из центральных ролей. Так, Ричард Фейнман в своих «Фейнмановских лекциях по физике» пишет, что это явление, «которое невозможно, совершенно, абсолютно невозможно объяснить классическим образом. В этом явлении таится самая суть квантовой механики».

Эксперимент с двумя щелями демонстрирует одно из центральных понятий квантовой физики — квантовую суперпозицию. Принцип квантовой суперпозиции утверждает, что если некий квантовый объект (например, фотон или электрон) может находиться в некоем состоянии 1 и в некоем состоянии 2, то он может находиться и в состоянии, которое является в некотором смысле частично и состоянием 1, и состоянием 2. Это состояние и называется суперпозицией состояний 1 и 2. В случае с щелями частица может пройти через одну щель, а может через другую, но если обе щели открыты, то частица проходит через обе и оказывается в состоянии суперпозиции «частицы, прошедшей через щель 1» и «частицы, прошедшей через щель 2».

Самым известным объектом, находящемся в состоянии квантовой суперпозиции, является кот Шрёдингера, который и жив, и мертв одновременно. Dhatfield / Wikimedia Commons

В 2012 году в работе, опубликованной в журнале Physical Review Letters, авторы обратили внимание, что принцип суперпозиции в этом случае зачастую понимают и даже объясняют в учебниках неправильно. Обычно говорят, что состояние частицы после прохождения двух щелей представляет собой суперпозицию ее состояний после прохождения каждой из щелей при закрытой другой щели, однако это не совсем так. Когда открыты обе щели, каждая из них оказывает влияние на другую и частица, вообще говоря, теперь проходит каждую из щелей не так, как проходила бы ее, если бы другая щель была закрыта. И хотя отличие невелико и его сложно измерить в эксперименте, оно может играть роль, если рассматриваются слабые эффекты. Кроме того, как оказалось, влияние щелей друг на друга можно усилить.

Влияние одной щели на другую на квантовом языке проще объяснять через одно из альтернативных описаний квантовой физики, разработанное тем же Ричардом Фейнманом. Согласно его подходу, известному как «интегралы по траекториям», при перемещении частицы из одной точки в другую она проходит сразу по всем возможным траекториям, соединяющим эти точки, но каждая траектория имеет свой «вес». Наибольший вклад дают траектории, близкие к тем, которые предсказывает классическая физика, — именно поэтому квантовые законы в пределе сводятся к классическим. Но и другие траектории тоже важны (см., рисунок в заглавии этой работы, В.К.).

Среди этих траекторий могут быть и такие, которые совершенно невозможны классически. Они, скажем, могут содержать участки, на которых частица движется в обратную сторону. В случае эксперимента с щелями это, например, траектории, которые сначала входят в одну щель, затем проходят через другую, а затем выходят через третью. Именно такие странные траектории и объясняют влияние одной щели на другую, потому что только они отсутствуют, когда одна из щелей закрыта.

Чтобы доказать наличие «неклассических» траекторий, Роберт Бойд с коллегами предложили усилить их влияние за счет возбуждения так называемых приповерхностных плазмонов. Плазмоны — это связанное состояние фотона и электрона в металле. За счет них свет оказывается как бы привязанным к поверхности металла и может эффективно распространяться вдоль нее на относительно большие расстояния. Существование плазмонов увеличивает влияние одной щели на другую и, соответственно, «вес» траекторий, идущих от одной щели к другой.

В эксперименте Бойда щели были вырезаны пучком ионов в слое золота, напыленного на прозрачное стекло. Поскольку золото хороший проводник, то в нем легко возбуждаются плазмоны.

Чтобы наблюдать влияние щелей друг на друга, экспериментаторы предложили провести следующий опыт. Сначала две щели из трех закрывают, и фотоны проходят только через одну щель. На экране в этом случае получается небольшая освещенная полоска. При этом используют источник света, ширина луча которого меньше расстояния между щелями. Поэтому когда щели открываются, то, согласно наивным представлениям, картина меняться не должна — ведь эти щели не освещаются. Однако из-за влияния щелей друг на друга существуют такие траектории, которые, войдя через освещаемую щель, выйдут из щели, которая не освещается, и создадут интерференционную картину. За счет плазмонов этот эффект усиливается, и в опыте хорошо видно изменение характера освещенности экрана. Это и доказывает существование «неклассических» траекторий.

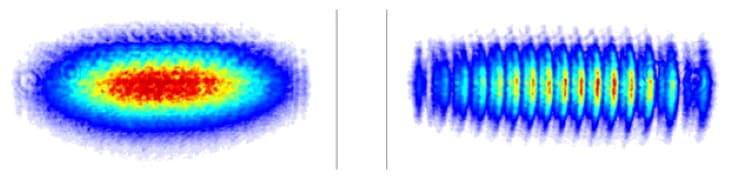
Сравнение картины, получаемой на экране в случае, когда открыта только одна щель (слева) и когда открыты все три щели (справа). O. S. Magaña-Loaiza et al., Nat. Commun

На данный момент не совсем понятно, могут ли эти исследования иметь какое-то значение для прикладных задач. Авторы работы надеются, что с помощью усиления неклассических траекторий можно создавать более эффективные протоколы работы устройств, основанных на явлении квантовой суперпозиции и интерференции, — например, квантовых компьютеров, предназначенных для симуляции реальных квантовых систем (так называемые, квантовые симуляторы).

Кроме того, учет неклассических траекторий важен для еще одного направления в современной фундаментальной физике. Одна из главных нерешенных проблем, стоящих перед учеными, — это объединение квантовой теории с теорией гравитации. На этом пути существуют принципиальные сложности, которые, как считают многие, можно преодолеть, только видоизменив или одну из этих теорий, или сразу обе. Поэтому сейчас идут поиски возможных расхождений реальности с предсказаниями этих теорий. Одним из направлений является поиск отклонений от принципа квантовой суперпозиции. Так, в 2010 году было опубликовано исследование, авторы которого пытались найти такие отклонения в трехщелевом эксперименте. Никаких расхождений не обнаружили, но эта статья спровоцировала упоминавшуюся выше работу 2012 года. Один из ее выводов заключался как раз в том, что в эксперименте 2010 года было использовано неправильное понимание принципа квантовой суперпозиции и это внесло свою долю неучтенной ошибки в измерения. И хотя величина этой ошибки была мала, эффект, который ищут ученые, тоже может быть невелик, поэтому в таких поисках вклад неклассических траекторий следует все же учитывать.

Источник: http://victorpetrov.ru/tryoxsh...

В.К. Казалось бы, какая связь между двумя этими публикациями кроме той, что и там, и там речь идёт о квантовой суперпозиции? Однако, это на первый взгляд. На самом же деле, эта связь существенная и значительная.

Начнём, пожалуй, с того, что при облучении щелей что частицами, например, электронами, что светом, картина получается приблизительно одна и та же. Даже, если облучение происходит одиночными электронами или одиночными квантами света, а не коллимированным пучком даже монохроматическим излучением на протяжении какого-то времени, картина особо не отличается от этой:

Если же мы теперь посмотрим на картинку в трёзщелевом эксперименте, где приведены картинки с одной и тремя щелями, то можно увидеть, что на изображении от одной щели хорошо просматривается некоторая дискретность - некоторое пространственное распределение квантов на экране. При похождении же света через две или более щелей, даже и безо всяких плазмонов, дискретность эта проявляется более отчётливо.

С чем это может быть связано? А связано это может быть с тем, на мой взгляд, что частицы в пучке или по отдельности не являют собой нечто идентичное - всегда между ними будет некое различие, которое выражается неким распределением.

Но, почему эти частицы проходят через разные щели, если расстояния между ними таковы, что эти частицы никак в другие, кроме той, в которую и направлены, не могли бы попадать?

А вот здесь мы и переходим к самому главному. Дело всё в том, на мой взгляд, что, много говоря о влиянии наблюдателя на ход эксперимента, мы совершенно упускаем из виду тот факт, что система излучатель-щели-экран формирует собственное пространство взаимодействия и именно поэтому, например, синие фотоны не петляют между щелями, а каждый пролетает по той траектории, по которой и осуществляется наибольшая связь в этой системе. И именно поэтому картинка от трёх щелей повторяет картинку от одной щели в каждой дискретизации, выражая тем самым, распределение частиц в потоке.

Говоря другими словами, изначально мы ничего не можем сказать о распределении частиц в потоке, но, как только появляются щели и экран - те самые наблюдатели, распределение тут же и проявляется.

И здесь кстати будет сказать, на мой взгляд, что всё описанное имеет место быть в любых экспериментах, в том числе и тех, которые проводят на коллайдере, сталкивая протоны друг с другом (я об этом ранее писал), и даже в нашей повседневной жизни, и в жизни вообще.

Поэтому, на мой взгляд, здесь очень важно понимать, вспомнив утверждение древних: Ничто только тогда становится Нечто, когда осознано.