Математическая смекалка. Новое решение известной старой задачи со спичками.

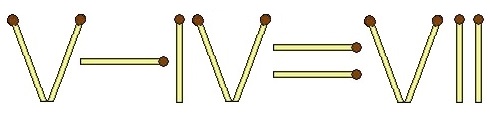
Обобщение очень старой классической задачи со спичками,  

VII = I  

в которой надо переложить одну спичку, чтобы неправильное выражение стало правильным (похожая задача – на картинке).  

Кажется из "Математической смекалки".  

(была такая хорошая книжка и в ней, насколько вспоминаю, эта классическая задача)  

--------------------------------------------------  

Даны два любых, но не равных друг другу числа.  

Эти числа записаны римскими цифрами с помощью обычных спичек, и имеют в своем составе хотя бы одну единственную вертикальную спичку.  

Между этими, не равными друг другу числами, с помощью спичек поставлен знак равенства.  

Например, классическая задача  

VII = I

Или

II = III

или

IX = X

или

XI=XX

и так далее.

Как переложить одну спичку, чтобы неправильное выражение стало правильным?

--------------------------------------------------

У задачи имеется (как минимум?) три класса общих решений.

Сможет ли кто-нибудь найти эти классы решений и классы чисел, на которых действуют эти решения?

* Кроме того, для одного из классов решений существует дополнительное единичное исключение в виде сочетания двух конкретных чисел.

Правда это исключение решается двумя другими классами решений. 

Решения - очень простые. Гораздо проще, чем классическое частное решение.

Тем не менее, несколько десятков лет люди решали классическую задачу, но так и не оставили следов о таких решениях.

Так что желающие могут размять свои мозги.

Авторский первоисточник обобщённой задачи

https://my.mail.ru/community/economics_sng/4BA3F51FCE8F98DF.html#4BA3F51FCE8F98DF