Передаю пламенный привет остолопам из РАН, РАО, РКС и всех Министерств просвещения и образования.

В статье используются фрагменты из кинофильма "Тот самый Мюнхгаузен", Мосфильм, 1979 год. Они имеют непосредственное отношение к тому, что написано в статье, так что все кинофрагменты смотреть обязательно.
Петр Иванович Дубровский, добросовестный инженер – исследователь, честный и непредвзятый частный научный детектив. d-pi@yandex.ru
Случилось так, что в ответ на мои сетования, что в школе неверно излагают второй закон Ньютона, вследствие чего почти никто из получивших "аттестат зрелости" не понимает истинного смысла импульса силы Ft, не понимает, что время t действия силы F на материальное тело массой m так же важно, как и величина силы F, так как в учебниках почти нет упоминаний ни об импульсе силы, ни о кол-ве движения, мне неожиданно прилетело по моему задранному вверх носу сразу от нескольких читателей документально подтверждённое опровержение моих слов:


Я со своей стороны выражаю искреннюю признательность этим внимательным читателям, потому что всего знать невозможно, часто даже не удаётся качественно перепроверить ту или иную информацию, поэтому , когда у меня находят реальные ошибки и указывают мне на них, я говорю за это "спасибо".
Соответственно, я разыскал этот учебник в Интернете, скачал его и принялся изучать, как же трактуется в нём закон сохранения количества движения (импульса) и какие задачи предлагается решать ученикам по этой теме. И внезапно я наткнулся в этом самом параграфе 39 на очень забавную задачу.
Но сперва давайте вспомним, по какой схеме должна правильно развиваться наука физика. Прежде всего, описывается некое явление:
ну и разумеется, приводятся некоторые доказательства достоверности этого явления, например "Я же - жив!" Затем проводятся эксперименты по проверке этого явления... пускай все они закончились неудачей, но истинных физико-теоретиков такие мелочи никогда не смущали:
Ну и наконец, самыми передовыми физико-теоретиками пишется научная работа (научный трактат), теоретически объясняющий это явление и эта новая теория начинает преподаваться в школах и вузах:
Автор научного трактата с нетерпением ожидает, когда у него "повысится индекс Хирша", а учащиеся с восторгом принимают теоретические объяснения новой, не ретроградной теории.
Какое отношение "вытаскивание себя за волосы из трясины... причем вместе с конём" имеет к уже упомянутому учебнику "Физика, 10 класс" за 2014 год (извините, я не смог найти более свежего, но, полагаю, и в новом учебнике остались старые задачи), спросите Вы? Да самое непосредственное!
Читаем задачу:
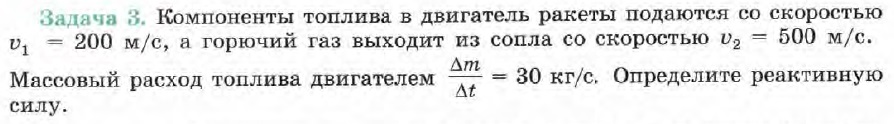
Читаем "авторское решение" этой задачи, прошедшее все возможные экспертизы:

Так вот, мне очень понравилась эта задача... а еще больше понравилось её "авторское решение"... Ведь правда, мы же не ретрограды какие, в самом-то деле. Эта задача, дорогие мои читатели, почти из того самого разряда замечательных задач - с какой силой и в продолжение какого времени надо дёрнуть самого себя за волосы, чтобы вытащить себя из трясины... вместе с конём.
Поэтому я поздравляю автора этой задачи Н.Н Сотского ... и редактора этого учебника профессора Н.А. Парфентьеву с замечательным научным открытием, которое просочилось в школьные учебники, но пока еще не было удостоено Шнобелевской премии.
Также можно поздравить академиков РАН, академиков РАО (Российской академии образования) и каких-то членов Российского книжного союза, которые провели научную, педагогическую и общественную экспертизы этой задачи и выдали положительные заключения, т.е. можно смело поздравить с присвоением звания "заслуженный остолоп" всех тех, кто поставил свои подписи под этими заключениями. К моему глубокому сожалению, я не знаю всех их поимённо, а то бы не преминул перечислить всех их в этой статье - ведь граждане должны знать своих героев!

Если кто всё еще не понял, в чем тут прикол этой задачи, то я попытаюсь объяснить максимально просто и доступно.
Дело в том, что для определения величины тяги, что есть реактивной силы, создаваемой ракетными двигателями, поднимающих ракету, наполненную компонентами ракетного топлива, всё выше и выше, совершенно безразлично, с какой скоростью и даже в каком именно направлении подаются в двигатель эти компоненты топлива.
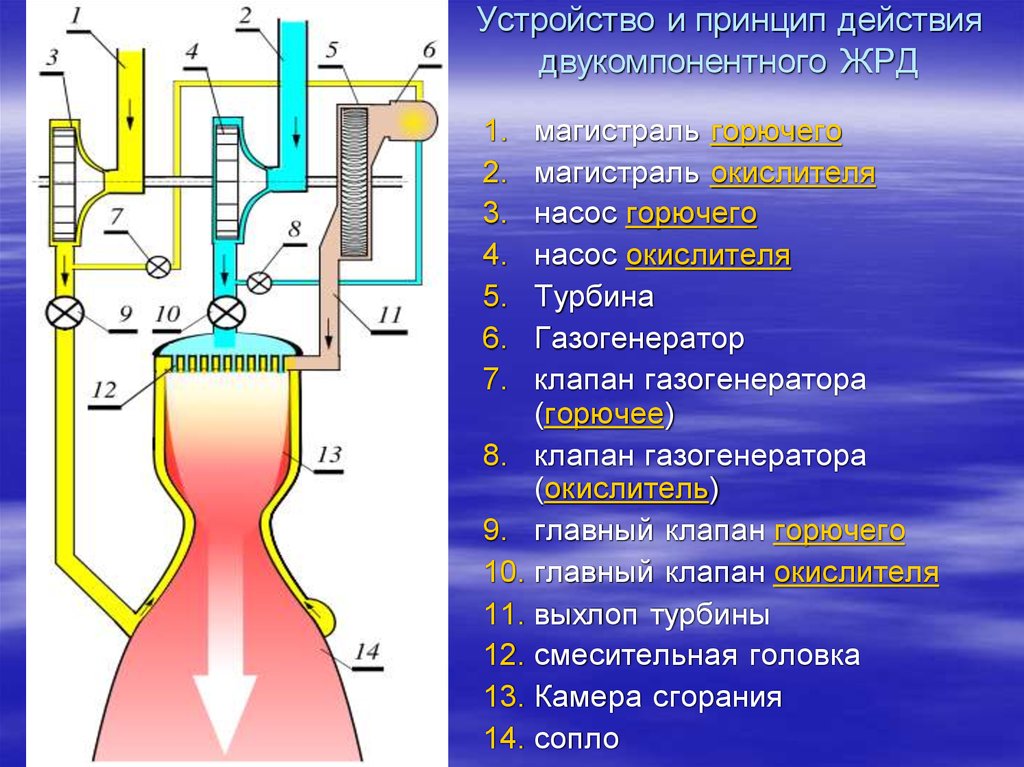
Например, вот на этой схеме показано, что разогнанное насосом 3 горючее, проходя главный клапан горючего 9, попадает в рубашку охлаждения камеры сгорания, где выполняется сразу две функции - охлаждается камера сгорания, что не позволяет ей расплавиться и нагревается горючее, чем повышается эффективность его использования. Так вот, в движение горючего в рубашке охлаждения, как это видно на схеме - противоположное тому направлению, которое придавал горючему насос горючего 3. Мне вот интересно, это, по мнению Н.Н. Сотского и прочих остолопов, тоже следует учитывать в расчётах? Из рубашки охлаждения разогретое горючее попадает в смесительную головку, где смешивается с окислителем, и уже откуда подаётся под давлением, создаваемым насосами 3 и 4, в камеру сгорания. В камере сгорания топливо сгорает, повышая давление внутри камеры. Это давление, по сути, и определяет величину тяги реактивного двигателя.
Если посмотреть на схему реального реактивного ракетного двигателя РД-180, то прекрасно видно, что насосы горючего (Fuel Pump) и окислителя (жидкого кислорода LOX Pump) расположены на уровне и даже ниже камеры сгорания, как быть в этом случае с расчётами по импульсам mv, граждане Н.Н. Сотский и эксперты из РАН, РАО и РКС?
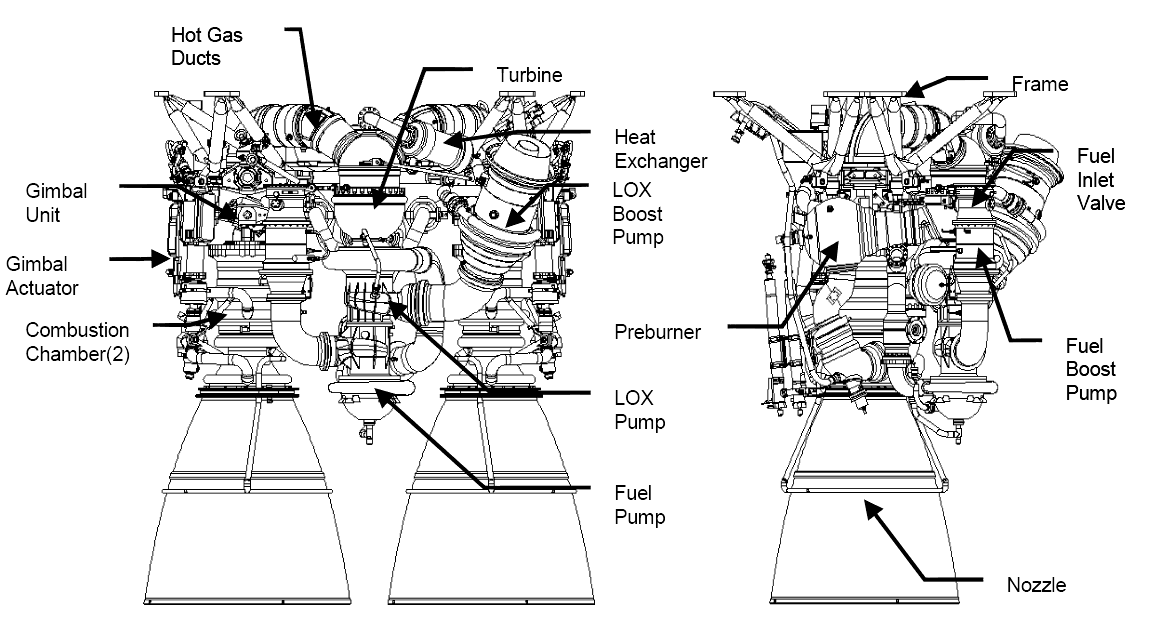
Надеюсь, это всем понятно?
Вернёмся к задаче. Так как массовый расход топлива по условиям задачи составляет 30 кг/с, а скорость исходящих из сопла газов - 500 м/с, то мы определяем импульс, который сообщает исходящий газ двигателю, а вместе с двигателем и ракете, В ТЕЧЕНИЕ ОДНОЙ СЕКУНДЫ, равным 15000 кг*м/с, т.е. 15 т*м/с.
Вспоминаем правильную формулу второго закона Ньютона Ft = Δ(mV). Это означает, что за каждую секунду, кол-во движения, сообщённое ракете с прикреплённым к ней ракетным реактивным двигателем, увеличивается на величину 15 т*м/с, а из этого следует, что сила тяги этого самого реактивного ракетного двигателя равна 15 тыс. Ньютонов. И ни одним Ньютоном меньше. Это, надеюсь, всем понятно? И моим читателям, и Н.Н. Сотскому, и даже остолопам-экспертам из РАН, РАО и общественникам из РКС? Если что непонятно, спрашивайте, не стесняйтесь. Физическое отделение наук РАН может пригласить меня провести среди академиков ОФН РАН несколько лекций с целью ликвидации вопиющей неграмотности в вопросах элементарной физики.
А как же насчёт перекачки топлива и жидкого кислорода внутри ракеты? Неужели это никак не влияет на движения ракеты? И вот сейчас необходимо, чтобы читатели на всякий случай проверили, включены ли их мозги или же нет.
Действительно, если бы перекачиваемое со скоростью 200 м/с топливо внутри ракеты никуда из ракеты не девалось, т.е. двигалось бы по закольцованному контуру, то мы тогда имели бы классическую задачу барона Карла Фридриха Иеронима фон Мюнхгаузена "Как вытащить себя за волосы вместе с конём из трясины". Но фишка в том, что компоненты топлива, прокаченные из резервуаров с керосином и окислителем, сгорают внутри камеры сгорания и не возвращаются назад.
Правильный ответ нам поможет найти упражнение 20, номер 3, параграф 20 из "Белого учебника по физике 9 класса", А.В. Пёрышкин, Е.М. Гутник. Дрофа, 2014 г. Задача такова: Человек сидит в лодке, покоящейся на поверхности озера. В какой-то момент он встаёт и идёт с кормы на нос. Что произойдёт при этом с лодкой? Объясните явление на основе закона сохранения импульса.
Цитирую ответ:

В случае с односторонней перекачкой компонентов топлива сверху вниз с темпом 30 кг/с и со скоростью 200 м/с, это будет придавать ракете с присоединённым двигателем, керосином и окислителем в её резервуарах ДОПОЛНИТЕЛЬНЫЙ ПРИРОСТ импульса в направлении полёта ракеты, и этот прирост будет равен 30 кг/с х 200 м/с = 6000 кг*м/с в каждую секунду полёта ракеты, то есть будет создавать дополнительную реактивную силу величиной 6 тыс. Ньютонов, способствуя подъёму ракеты, а не замедляя этот подъём.
Таким образом полная подъёмная сила, действующая на ракету, будет равна 15 тыс. Ньюонов + 6 тыс. Ньютонов = 21 тыс. Ньютонов, а не 9 тыс. Ньютонов, как получилось в многомудрых расчётах автора задачи Н.Н. Сотского и чего не увидели остолопы-эксперты. Тщательнее надо, ребята. Ведь вам всем за экспертизу учебников деньги явно заплатили - так что, получается, что напрасно заплатили? Вы даже такой очевидной глупости не увидели? Ни одна из экспертиз?
Впрочем, это не единственный пример глупости и ограниченности мышления авторов школьных учебников физики, академиков РАН и РАО, чиновников из различных Министерств просвещения и образования...
Мне вот что интересно - а в каком году в учебниках впервые появилась эта задача? И убрана ли эта задача (или хотя бы её крайне бестолковое решение) из учебников более поздних изданий? У меня нет возможности скупать все учебники физики. Поэтому я буду благодарен читателям за подробную информацию.
Подписывайтесь, чтобы не пропустить мои дальнейшие находки глупостей в школьных учебниках и самим лучше понимать физику. Репосты этой статьи на различных сайтах приветствуются (с указанием автора)!











Оценили 12 человек
16 кармы