
Толчком к написанию этой статьи послужила другая статья – о числе 108 (https://cont.ws/@Sage/1374746). Дескать, и такое оно, и сякое, со всех сторон и круглое, и квадратное. Причём, одновременно!
С точки зрения человека, немного умеющего мыслить, – там одна вода. По сути, число 108 обладает только одним свойством: внутренний угол правильного пятиугольника в градусах равен 108. Всё остальное притянуто за уши. Причём, с усилием, достойным лучшего применения.
Пользуясь случаем, расскажу вам о своих изысканиях в этой области – в области поиска интересных свойств у чисел, чем я по молодости грешил. Да и сейчас мимо темы обычно не прохожу.
Однажды я узнал о существовании совершенных и сверхсовершенных чисел.
Совершенные числа – это такие числа, сумма всех собственных делителей которых равна самому числу.
Собственным делителем числа называется любой делитель числа, отличный от самого числа. У простых чисел только один собственный делитель – единица.
Примеры совершенных чисел: 6, 28, 496, 8128, 33 550 336, 8 589 869 056, и т.д.
Собственные делители числа 6: 1, 2, 3. Их сумма (1+2+3) равна 6, т.е. самому числу.
Сверхсовершенные числа в математической терминологии называются избыточными.
Избыточные (сверхсовершенные) числа – это числа, сумма всех собственных делителей которых больше самого числа.
Первым сверхсовершенным числом является число 12: 1 + 2 + 3 + 4 + 6 = 16 (>12)
Узнав о том, что существуют сверхсовершенные числа, я подумал: а что дальше? Полученное из 12-ти число 16 – какое оно? Несовершенное, совершенное или сверхсовершенное? Оказалось – недостаточно совершенное – сумма его собственных делителей равна 15. А у 15-ти – 9, и таким образом я получил последовательность:
12 16 15 9 4 3 1
Назвал эту последовательность «Жизнью числа», написал программу на Visual Basic и начал исследовать жизнь различных чисел. Нашёл немало интересного (как теперь знаю, уже известного, но тогда это были мои собственные открытия). Я нашёл, что существуют (в терминах современной математической теории):
Избыточные числа
Недостаточные числа
Слегка избыточные числа (квазисовершенные числа)
Слегка недостаточные числа
Дружественные числа
Полусовершенные числа
Кому интересно, могут почитать об этих числах в Википедии. Однако, не это не главное. Самым интересным для меня оказалось то, что у некоторых чисел – очень насыщенная внутренняя жизнь. Причём, порой ничем не примечательное число может иметь очень богатую внутреннюю жизнь.
В те времена, когда компьютеры были не так сильны, я не нашёл «конца» жизни у некоторых чисел. Сейчас вернулся к этой теме и просчитал их ещё раз. И даже сейчас я не нашёл конца у числа 720, которое в настоящий момент является рекордсменом по «длине жизни». Впрочем, по порядку.
12 – первое сверхсовершенное число.
Сверхсовершенные (избыточные) числа: 12, 18, 20, 24, 30, 36, 40, … 60, … 100, … 120, 126, 138, 140, … 180, … 360, … 720, …
Жизнь чисел бывает самой разной. Лучше всего её увидеть в графическом виде.
Жизнь числа 120 (максимум - 32 571):
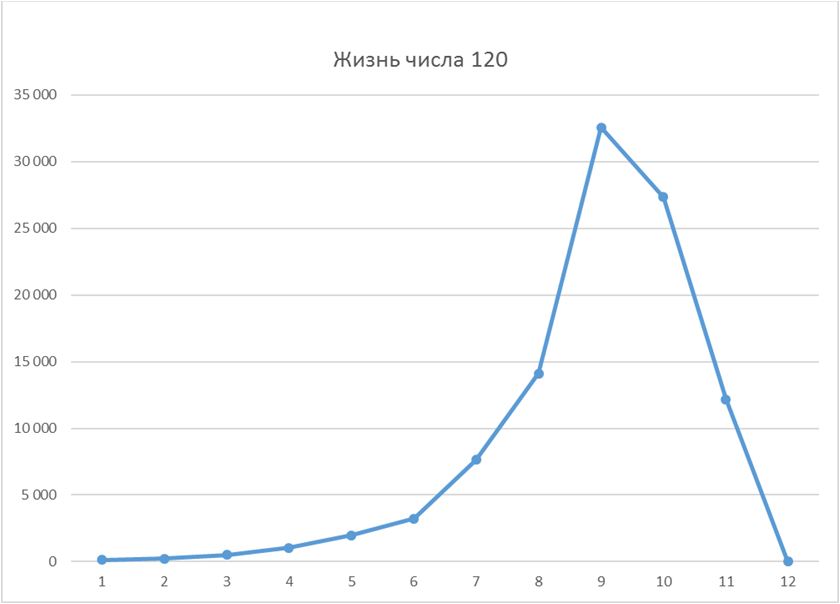
Жизнь числа 480 (максимум – 321 836):
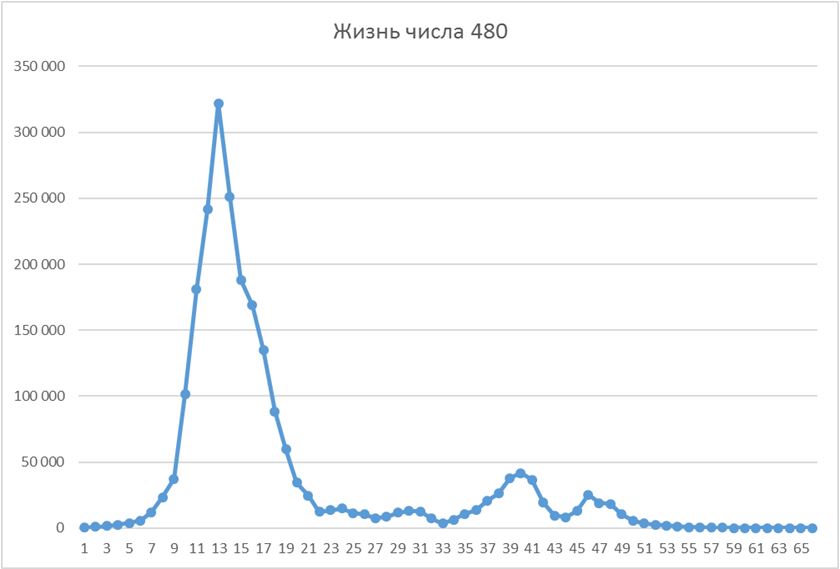
Жизнь числа 742 (максимум - 890):
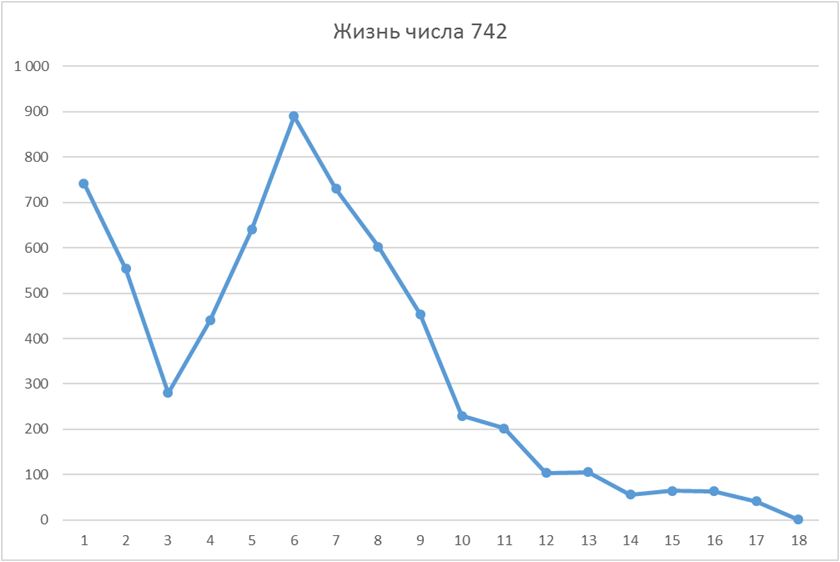
Жизнь числа 642 (в максимуме - 18 632 и 18 628):
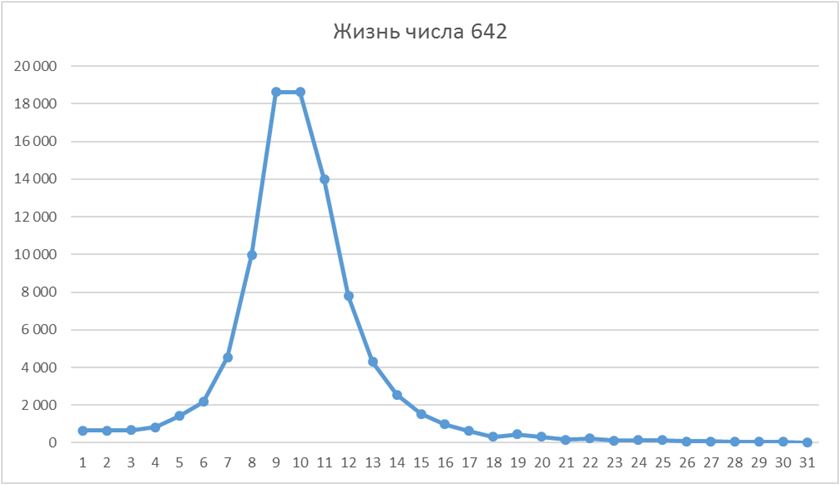
138 – наиболее сильно удивившее меня число. Его собственные делители ничем не примечательны: 1, 2, 3, 6, 23, 46, 69. Их сумма равна 150. А у 150-ти – 222. И т.д. Всю жизнь числа 138 мне удалось посчитать лишь недавно. Вот она:
138
150
222
234
312
528
960
2 088
3 762
5 598
6 570
10 746
13 254
13 830
19 434
20 886
21 606
25 098
26 742
26 754
40 446
63 234
77 406
110 754
171 486
253 458
295 740
647 748
1 077 612
1 467 588
1 956 812
2 109 796
1 889 486
953 914
668 966
353 578
176 792
254 128
308 832
502 104
753 216
1 240 176
2 422 288
2 697 920
3 727 264
3 655 076
2 760 844
2 100 740
2 310 856
2 455 544
3 212 776
3 751 064
3 282 196
2 723 020
3 035 684
2 299 240
2 988 440
5 297 320
8 325 080
11 222 920
15 359 480
19 199 440
28 875 608
25 266 172
19 406 148
26 552 604
40 541 052
54 202 884
72 270 540
147 793 668
228 408 732
348 957 876
508 132 204
404 465 636
303 708 376
290 504 024
312 058 216
294 959 384
290 622 016
286 081 174
151 737 434
75 868 720
108 199 856
101 437 396
76 247 552
76 099 654
42 387 146
21 679 318
12 752 594
7 278 382
3 660 794
1 855 066
927 536
932 464
1 013 592
1 546 008
2 425 752
5 084 088
8 436 192
13 709 064
20 563 656
33 082 104
57 142 536
99 483 384
245 978 376
487 384 824
745 600 776
1 118 401 224
1 677 601 896
2 538 372 504
4 119 772 776
8 030 724 504
14 097 017 496
21 148 436 904
40 381 357 656
60 572 036 544
100 039 354 704
179 931 895 322
94 685 963 278
51 399 021 218
28 358 080 762
18 046 051 430
17 396 081 338
8 698 040 672
8 426 226 964
6 319 670 230
5 422 685 354
3 217 383 766
1 739 126 474
996 366 646
636 221 402
318 217 798
195 756 362
101 900 794
54 202 694
49 799 866
24 930 374
17 971 642
11 130 830
8 904 682
4 913 018
3 126 502
1 574 810
1 473 382
736 694
541 162
312 470
249 994
127 286
69 898
34 952
34 708
26 038
13 994
7 000
11 720
14 740
19 532
16 588
18 692
14 026
7 016
6 154
3 674
2 374
1 190
1 402
704
820
944
916
694
350
394
200
265
59
1
В максимуме получено число 179 931 895 322. Длина жизни (длина полученной последовательности), включая само число – 178.
Скорость роста и падения значений ряда местами близко к экспоненциальному:

При этом небольшое утолщение в районе 70-ых значений – сам по себе тоже немаленький пик:
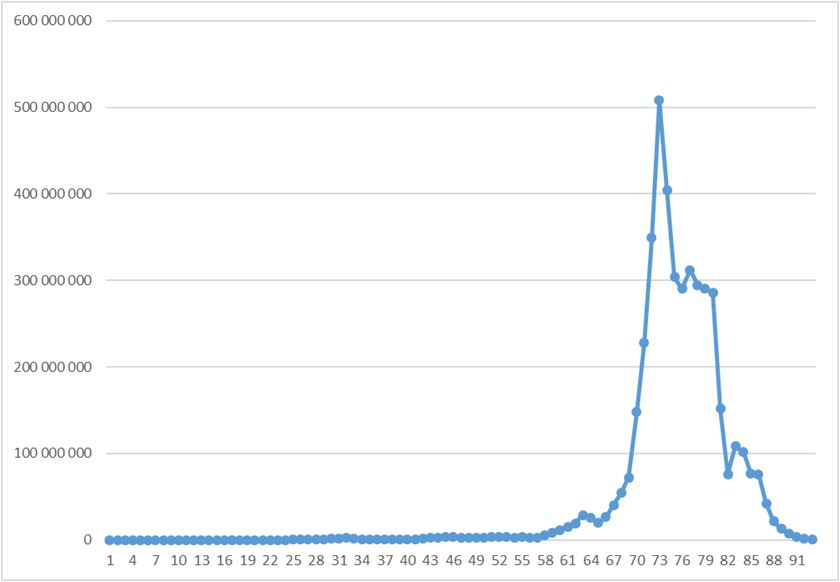
Чтобы сгладить перепады в жизни числа, возьмём логарифм полученных значений:
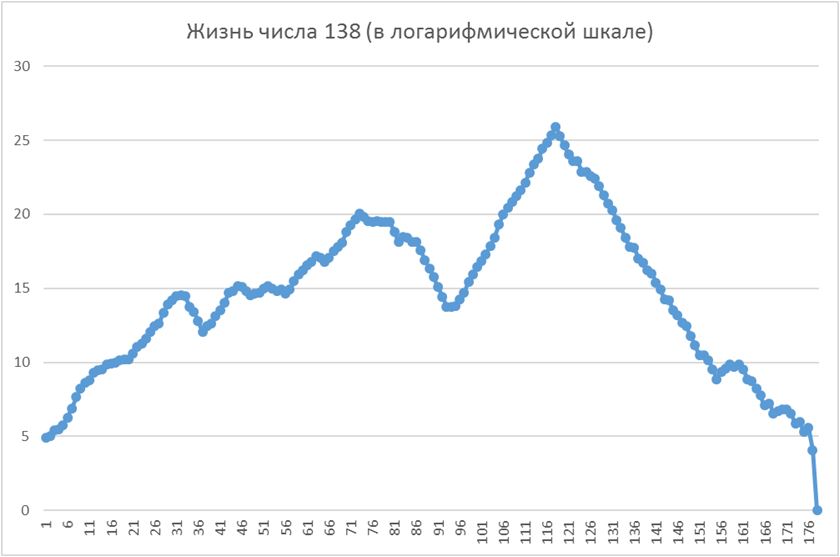
На участке от 93-го значения до максимального (значение 118) зависимость очень близка к экспоненциальной со степенью, местами близкой к 1,5. Т.е. отношение рядом стоящих чисел ряда почти точно равно 1,5. Самые близкие значения: 1,5000043767, 1,5000000805, 1,5000000536, 1,5002064735, 1,5000000015:
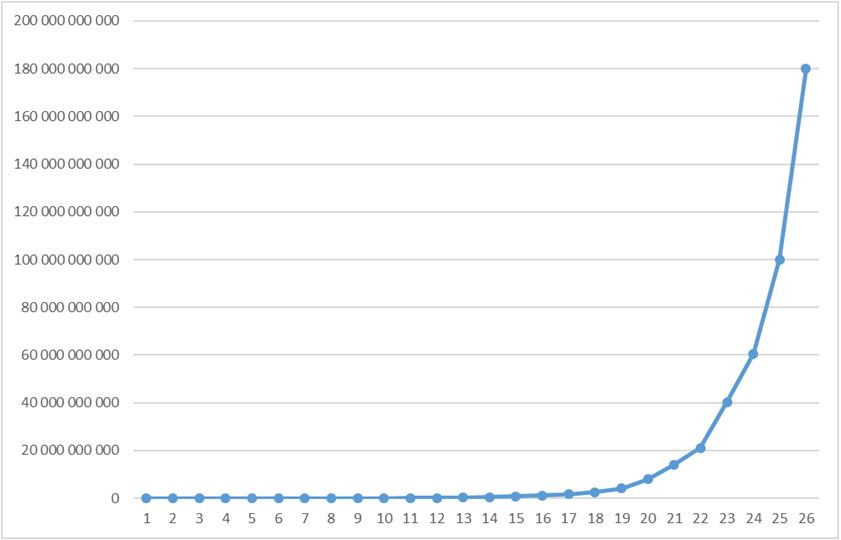
А на этапе падения кривой (перед вышеописанным взлётом, но не только там) степень близка к 0,5: 0,50296810, 0,50673870, 0,50000162.
Одной из самых длинных жизней из сравнительно небольших чисел обладает число 720 (360 х 2). Последовательность состоит из 191 числа, а максимальное значение исчисляется квадрильонами:
36 445 367 869 087 800:
720
1 698
1 710
2 970
5 670
11 754
13 752
23 688
51 192
94 008
141 072
223 488
427 526
272 098
147 194
73 600
116 120
145 240
181 640
250 360
365 240
494 440
646 040
857 320
1 071 740
1 235 572
1 093 104
1 966 472
1 735 828
1 311 104
1 301 116
987 044
840 796
789 140
1 134 124
951 316
812 684
620 860
719 780
958 540
1 237 892
1 046 908
808 932
1 078 604
808 960
1 156 640
1 576 300
2 157 836
1 646 524
1 635 524
1 486 924
1 127 324
1 024 924
789 476
592 114
302 954
151 480
238 760
314 200
416 780
665 140
931 532
1 165 108
1 165 164
2 522 772
5 218 668
11 903 892
25 427 052
53 825 940
132 775 020
331 001 748
760 541 292
1 492 916 628
2 490 326 636
5 183 606 260
7 370 428 940
10 560 940 852
12 481 112 588
12 481 112 644
17 623 960 508
20 935 668 292
25 605 989 948
30 285 997 252
30 573 080 188
34 370 987 924
39 658 833 004
41 211 587 732
41 211 587 788
42 695 114 924
53 420 518 564
53 420 518 620
131 770 616 964
220 630 419 324
433 833 337 476
968 456 265 084
2 100 700 764 036
4 076 359 821 114
5 241 034 055 814
5 337 199 819 626
5 337 199 819 638
6 979 141 213 722
8 147 569 309 254
9 516 864 662 658
11 103 131 607 930
19 721 291 643 270
42 357 371 012 730
71 543 356 060 590
121 564 608 079 410
206 732 590 044 966
258 936 054 156 522
302 135 189 842 458
487 524 897 248 742
571 581 342 231 066
666 844 899 269 616
1 279 728 304 928 780
2 513 206 992 836 010
4 880 141 275 173 070
7 726 890 352 357 480
13 769 727 091 931 400
14 973 900 865 721 200
27 505 094 545 817 300
36 445 367 869 087 800
31 889 696 885 451 800
15 948 418 727 906 100
8 799 127 574 017 270
5 780 231 679 986 320
2 898 674 919 482 850
1 482 596 328 952 340
806 143 636 415 978
575 816 883 154 294
287 908 441 577 150
248 301 335 229 250
216 812 581 415 582
110 503 352 862 562
70 973 108 494 430
56 778 486 795 562
41 059 244 737 238
37 356 288 988 522
26 728 513 811 798
14 761 479 258 202
9 917 154 796 838
5 036 957 229 082
2 520 587 315 174
1 260 309 373 186
651 395 856 074
334 344 776 026
181 254 214 670
145 105 289 410
116 095 329 590
95 399 615 434
47 731 154 774
23 865 577 390
19 258 918 514
12 330 904 366
7 846 939 178
4 887 146 074
2 531 895 206
1 265 947 606
1 156 609 322
736 024 150
695 142 062
361 854 994
181 589 486
116 174 938
74 998 022
48 284 410
38 851 502
19 470 874
9 735 440
18 762 736
17 590 096
18 277 648
17 135 326
10 638 098
6 092 398
3 749 210
3 182 446
1 601 594
807 994
584 486
431 578
334 502
238 954
122 234
87 334
53 786
26 896
26 517
8 843
277
1
Ниже - график последовательности в логарифмическом масштабе:
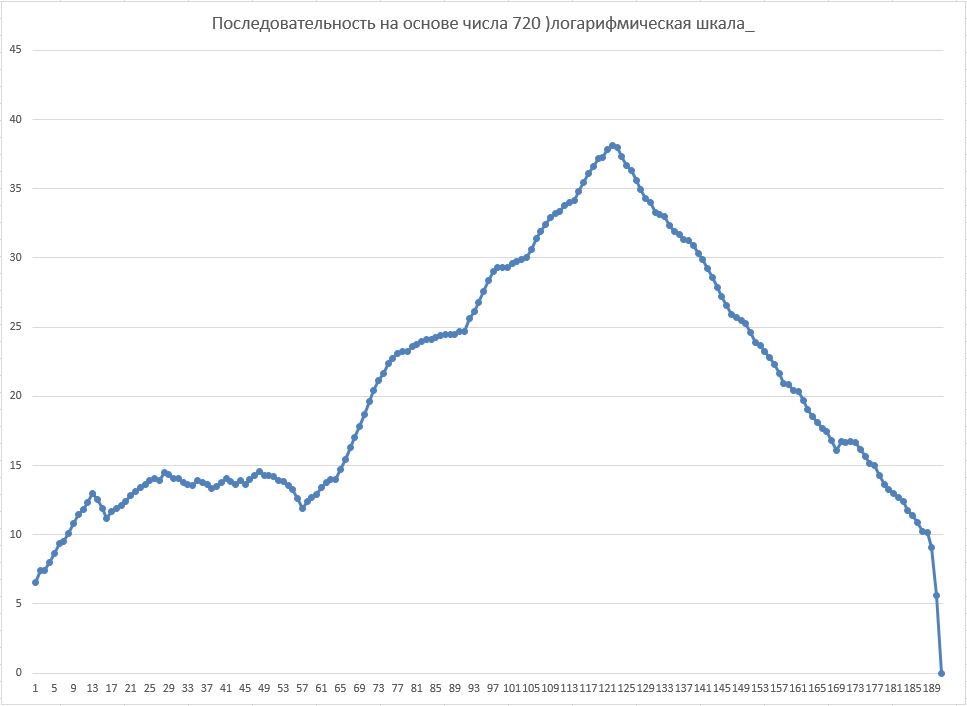
Также любопытно, например, что в жизни числа 720 есть последовательность из пяти чисел, заканчивающихся на 24:
1 646 524
1 635 524
486 924
1 127 324
1 024 924
Жизни чисел бывают связаны не только «дружественными», а более сложными узами – числа, как ручьи, могут сливаться в реки. Например, числа 138, 150, 222, … через пару-тройку шагов сливаются в одну реку (получают идентичные последовательности, начиная с числа 312):
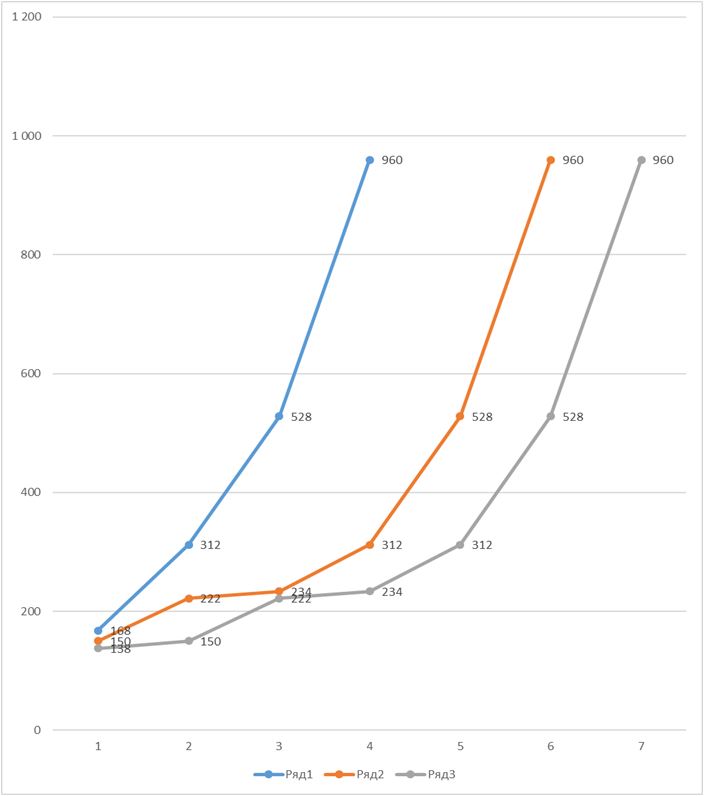
Таким образом, все числа, которые приходят к повторению последовательности других чисел, имеют разные корни, но общую судьбу. При этом основная линия судьбы принадлежит наименьшему числу. В данном примере – числу 138.
Ещё из интересного. Суммой делителей числа 720 является число 1698. Также это число является третьим в ряду, образованным от числа 1044. Но это же число является первым в ряду, образованным от чисел 1 326, 1 422 и 1 686. Т.е. сумма делителей чисел 720, 1 326, 1 422 и 1 686 равна 1698:
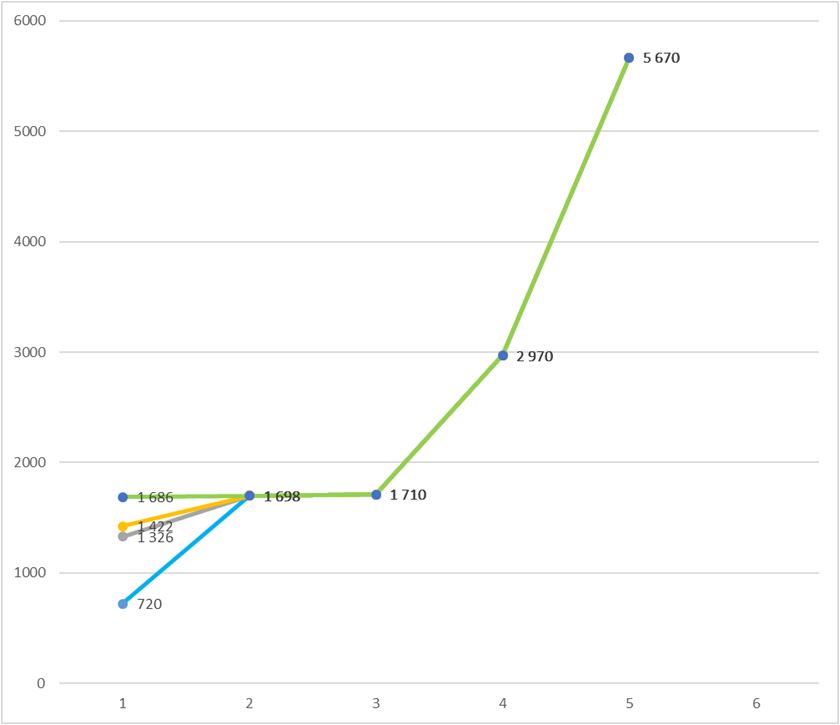
Уверен, что интересного в жизни чисел ещё немало. Я же только так, по верхам нахватал :)














Оценили 22 человека
41 кармы