Пазлы Вселенной. Фракталы

20:23, 06.06.2023

«Кто про что, а вшивые про баню» (с)… Так живем ли мы в «Матрице», или не живем? И какая она из себя? Одноименный фильм «Матрица» (с продолжениями) братьев Вачовских (или все-таки сестер?))), в свое время всколыхнул «общественность» всего мира по этой теме - поставил частокол вопросов по ее пластам, но на большинство из них не ответил. И, как водится в таких случаях, завернул интригу. Народ завелся. Основная волна обсуждений, конечно, схлынула, но латентно будоражит мозг неугомонных, вспыхивая брызгами в океане интернета. А о какой вообще матрице речь? Что это вообще за матрица такая?

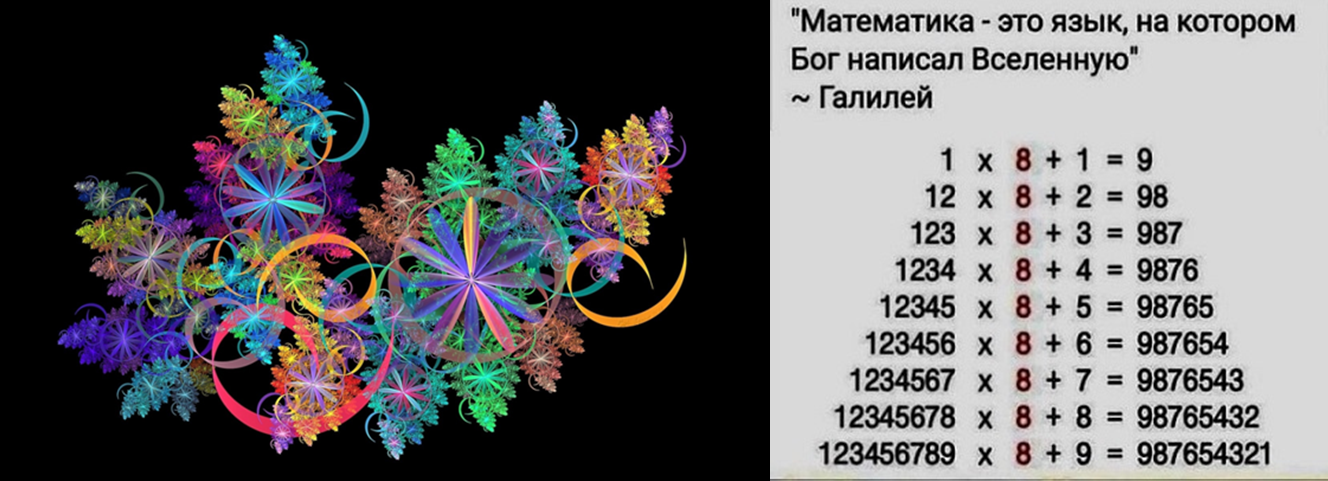
Матрица… это ведь что-то из математики… кажись. А «математика – это язык, на котором Бог написал Вселенную», - фраза, которую недавно (|:-)) ) кто-то из ныне живущих современников Галилея в своих воспоминаниях ему же и приписал!)) Не спорю, не присутствовала, им видней. Соглашусь.

Но ведь потрясающе красиво!

Ну а кто, кроме Бога это мог сделать? … Математика – это же язык Разума: логика, формулы, алгоритмы – это все его атрибуты. «Само-само» логике не подчиняется - это же хаос, так ведь?! А вот логика оперирует последовательностью причинно-следственных связей, двигаясь от исхода к цели. А если есть Цель, значит - есть и ЗАМЫСЕЛ! Кроме того, при движении к цели есть коридор ограничений (ресурсов, например) – ими служат законы природы, законоМЕРНОСТИ. Вот с мерностями математика и имеет дело!

Посмотрите на эту завораживающую магию последовательностей чисел:

В поисках «теории всего»

Самая древняя наука, понадобившаяся человечеству в чисто практических целях, это была – геометрия: участок там размежевать, дом построить, ну и всяко-разно. А от земли глаза рано или поздно устремлялись к небу… Какова геометрия Вселенной?

Как и многие науки, геометрия тоже проходила свои стадии развития: линейную, нелинейную и фрактальную, которые опираются на трех гигантов/колоссов - Евклида Александрийского, Николая Лобачевского и Бенуа Мандельброта. Каждая из трех была призвана решать свои задачи, делая гигантский скачок в познании мира.

Начиная с середины 20-ого века самой сложной и перспективной задачей теоретической физики является поиск так называемой «теории всего», которая объединит в себе общую теорию относительности и квантовую механику, тем самым дав точное объяснение всем наблюдаемым физическим явлениям. На роль такой теории претендуют многочисленные теории струн, теория квантовой петлевой гравитации и многие другие.

Профессор MIT (Массачусетского технологического института) Макс Тегмарк в своей книге «Наша математическая Вселенная» призывает нас задуматься о самом удивительном свойстве всех существующих физических теорий, которое обычно люди считают само собой разумеющимся — все наши физические теории описываются математикой.

С точки зрения эмпиризма (философия первичности материи по отношению к идее) в этом нет ничего удивительного - человек изобретал язык математики, наблюдая за реальным миром. Мы изобрели цифры и счет, чтобы считать предметы, мы изобрели геометрию, чтобы строить прочные здания. Со временем наши математические инструменты становились все более сложными и отдаленными от повседневных нужд — мы изобретали дифференциалы, интегралы, математический анализ, теорию групп, топологию. Но, в конце концов, мы всегда находили физические явления, которые поразительно хорошо описывались с помощью этих самых инструментов.

Но давайте взглянем на математичность физических законов с точки зрения идеализма (философия первичности идеи по отношению к материи). Все математические законы живут в пространстве идей и не зависят даже от существования нашей Вселенной. Если даже ничего не существовало бы, дважды два все также равнялось бы четырем. Рождение галактик и звезд, движение планет, химические реакции и генетические мутации строго следовали математическим формулам задолго до появления людей. Мы лишь открыли эти законы, но не изобрели их.

Так что же будет с теорией относительности, квантовой механикой или пресловутой «теорией всего», если мы выкинем из них всю словесную шелуху, вроде слов «квант», «пространство», «свет». Там останутся только формулы, и ничего больше.

И в этом месте рассуждений Макс Тегмарк задает интереснейший вопрос: что может полностью описываться чистой математикой? И он дает на него единственно разумный ответ. Чистой математикой может быть описана лишь сама чистая математика*. Таким образом, Тегмарк приходит к одной из возможных гипотез: вся наша Вселенная — это математическая структура.

*Примечание: вот тут я с уважаемым несогласная)) – чистой математикой может быть описана не сама чистая математика, а ОБРАЗ! Геометрия – это же контуры, т.е. визуализация ОБРАЗОВ (=смыслов), пазлов всего. А сама математика – это только инструмент, и не более того.

Сначала эту структуру описывали с помощью линейной геометрии Евклида и многогранников по Платону.

Евклид Александрийский (365-300 гг. до н.э.) - древнегреческий математик

«Начала» Евклида являются, наверное, самой знаменитой и значимой книгой в истории науки. Достаточно сказать, что геометрию по ней преподавали более двух с лишним тысячелетий. В целом и нынешнее обучение следует положениям Евклида, а геометрия, которую мы используем в повседневной жизни, называется евклидовой. Книга этого ученого древности строится на аксиоматическом принципе. В начале ее дается ряд постулатов и аксиом, считающихся бесспорными, а из них с помощью строгих рассуждений выводятся новые положения, именуемые теоремами. Среди всех аксиом Евклида особое внимание ученых привлекал пятый постулат.

Если все остальные интуитивно понятны и сформулированы вполне ясно, то определение пятого постулата (звучащее в упрощенном виде: «Через не лежащую на данной прямой точку на плоскости можно провести одну и только одну прямую, параллельную данной») вызывала недоумение. У математиков возникло предположение, что утверждение это на самом деле теорема, то есть его можно доказать, беря за основу другие аксиомы. На протяжении веков многие великие математики — Птолемей и Омар Хайям, Ламберт и Лагранж — пытались доказать это утверждение. Однако успеха никто не достиг, и в 1816 Гаусс разочарованно писал: «В области математики немного проблем, над которыми так много работали бы, как над пробелом в началах геометрии. И все-таки мы, если признаться откровенно, за две тысячи лет не ушли дальше Евклида.

Если мы посмотрим на то, что нас окружает, то условно сможем разделить все на две части: то, что создано человеком и то, что создала природа. То, что построено человеком — построено по постулатам евклидовой геометрии (круги, треугольники, квадраты, ромбы и т.д.). Но чем и как описать деревья, горы, реки? Как описать все то, что создала природа? Да, конечно, можно описать все, используя простые фигуры, меняя их масштаб, и положение, относительно друг друга ...что-то подсказывает, что мир бы выглядел как в игре Майнкрафт. Но, если серьезно, то попытка описать мир таким принципом — это лишь попытка смоделировать, но не описать все так, как оно есть.

Потом, уже в конце XIX века - с помощью нелинейной геометрии Лобачевского усложнили взгляд на геометрию природы. Образ стал выпукло-вогнутым. Это значительно приблизило наши представления к реальностям окружающего мира.

Лобачевский Николай Иванович (1792-1856)

Английский математик Уильям Клиффорд: «У Коперника и Лобачевского имеется интересная общая черта — оба они славяне по происхождению. Каждый из них произвел революцию в научных воззрениях, и обе эти революции имеют громадное значение — это революции в нашем понимании Космоса».

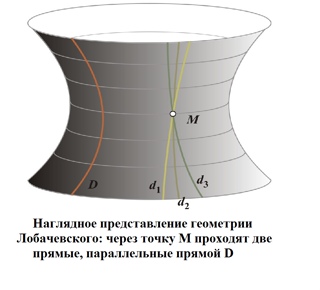
11 февраля 1826 навсегда осталось в истории математики. Именно в этот день в Казанском университете на очередном заседании физико-математического отделения Лобачевский зачитал доклад, в котором определил основные постулаты новой геометрии. Согласно его выводам являлось возможным построение геометрии, отрицающей пятый постулат Евклида. Самые простые свойства ее заключались в том, что через одну точку можно было провести множество прямых, не пересекающих заданную, а углы треугольника в сумме могли быть меньше 180 градусов. Разумеется, это находится в противоречии с нашими «бытовыми» представлениями, однако подобный мир, действительно оказался реализуем, соответствуя и законам физики, и логике. Коллеги же в открытии Николая Ивановича, совершившего переворот в представлении о природе пространства, не разобрались и, дабы поберечь самолюбие товарища, решили не давать никаких отзывов.

Лобачевский же будучи уверен в своей правоте руки не опустил. В 1829 и в 1830 в «Казанском вестнике» он публиковал мемуар (как тогда называлась научная статья) под названием «О началах геометрии», который стал первым печатным вариантом новой теории. Далее последовала «Воображаемая геометрия», затем «Новые начала» и, в итоге, «Исследования по теории параллельных». В предисловии одной из работ великий ученый так сформулировал свою главную идею: «Всем ведомо, что теория параллельных в геометрии является до сих пор несовершенной. Тщетное старание со времен Евклида заставило меня думать, что в понятиях самих еще не содержится той истины, которую желали доказать… Основное мое заключение допускает наличие геометрии в более широком смысле, нежели ее нам представил Евклид». Стоит подчеркнуть, что Лобачевский не опровергал работ древнегреческого математика, а доказывал вероятность существования геометрии на базе иного предположения о природе параллельности. В частности, Николай Иванович считал, что его — неевклидова — геометрия может работать в микромире, то есть на молекулярном уровне.

Наверняка, публикуя свои работы, Николай Иванович знал, что встретит некоторое непониманием а, возможно, и насмешки. Однако математик едва ли ожидал, что все они сольются в единый громкий хор. В ученом мире развернулась настоящая травля Лобачевского, академик Михаил Остроградский (к слову, самый видный российский математик той эпохи) оставил следующий уничижительный отзыв об одной из его работ: «По-видимому, автор задался целью таким образом писать, чтобы его было невозможно понять. И он этой цели достиг — большая часть его книги осталась для меня столь же неизвестной, как если б я ее никогда не видал…». Если в трудах не разобрались первые математики страны, то, что уж было говорить об остальных.

Из всех российских ученых лишь профессор механики Петр Котельников выразил уверенность в том, что открытие Николая Ивановича еще найдет своих ценителей. К слову, не найдя на родине поддержки, Лобачевский опубликовал свои труды на немецком языке. Но и в Европе ученый, по сути, нашел единственного читателя, зато какого! Им оказался Карл Гаусс, восхищенный работами русского ученого и ходатайствовавший об избрании его членом-корреспондентом математического общества в Геттингене.

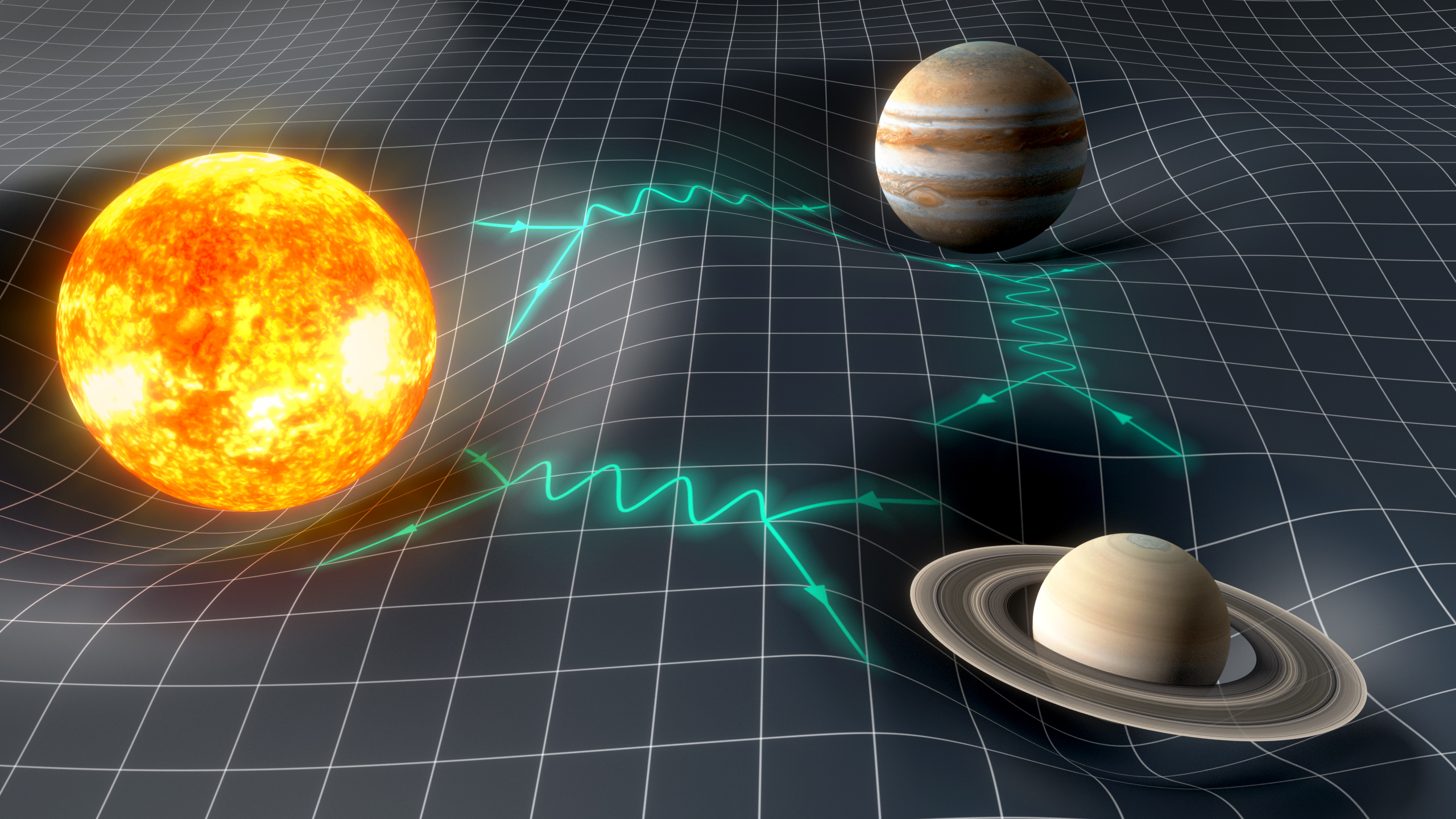
Николай Иванович не дожил до триумфа своих трудов всего десять-двенадцать лет. Очень скоро ситуация в науке изменилась коренным образом. Появление модели Клейна обосновало тот факт, что геометрия Лобачевского настолько же непротиворечива, как евклидова. Осмысление того, что геометрия древнего ученого имеет полноценную альтернативу, произвело на научный мир огромное впечатление, придав импульс множеству других идей, как в физике, так и в математике. В частности, замечательно «подошла» геометрия Лобачевского к созданной Эйнштейном общей теории относительности, одним из основных положений которой является искривление времени-пространства.

Все из бита

Макс Тегмарк не был первым, кто пришел к идее математичности Вселенной. Задолго до него эту идею выдвигал знаменитый американский физик, научный руководитель Ричарда Фейнмана, Хью Эверетта и Кипа Торна, а также автор терминов «черная дыра» и «кротовая нора» - Джон Уилер.

В своей статье «it from bit» Джон Уилер задумывался над тем фактом, что все свойства элементарных частиц вроде массы, заряда, спина, цвета, «странности» и «красоты» - не имеют никакого собственного смысла, а лишь проявляются при взаимодействиях с другими частицами. Таким образом, все эти свойства являются, по сути, битом информации в некоторой математической структуре.

«Всё из бита» символизирует идею, что всякий предмет и событие физического мира имеет в своей основе — в большинстве случаев в весьма глубокой основе — нематериальный источник и объяснение; то, что мы называем реальностью, вырастает, в конечном счёте, из постановки вопросов «да-нет» и регистрации ответов на них при помощи аппаратуры».

Если упростить высказывание Уилера, то получим: «Вначале было СЛОВО»** - как гласит Библия, или по-современному – вначале был КОД!

**Примечание: лично мне все же ближе такое определение – «Вначале был ОБРАЗ». А СЛОВО=КОД - это оцифровка ОБРАЗА.

Чтобы вы лучше поняли, что имел в виду Джон Уилер, приведем вам в пример картинку из книги Макса Тегмарка о том, как отношения между точками пространства (ребра куба) можно представить в виде матрицы битов:

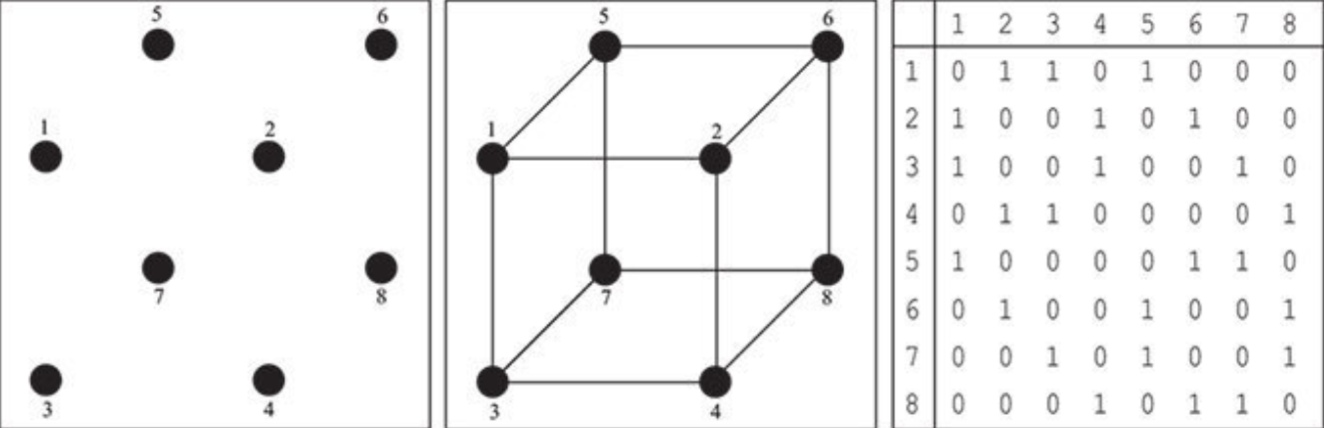
Сами вершины этого куба, обозначенные индексом от 1 до 8, не несут никакого смысла, а вот матрица отношений между ними (ребер куба) уже обладает некоторыми уникальными свойствами: например, вращательной симметрией. Наша Вселенная, конечно же, устроена на порядки сложнее куба, но в ее основе лежат те же самые принципы. Поняв это, мы можем двигаться дальше. Но двигаться дальше не получалось, так как для расчетов не хватало мощностей вычислительных средств. Они появились во второй половине ХХ века.

Инфляционная модель Вселенной и фракталы

Если мы все-таки живем в математической модели, то в какой?

Посмотрим на нашу Вселенную: она состоит из множества скоплений миллиардов галактик, галактики состоят из миллиардов звезд, у многих звезд есть несколько планет, а у многих планет есть некоторое количество спутников. Более того, согласно гипотезе вечной инфляции, являющейся объяснением и расширением инфляционной модели развития Вселенной, в отдаленном от нас пространстве ежесекундно происходят миллионы «больших взрывов», порождающих свои пузыри Вселенных, или фракталов - «по образу и подобию»!! Многообещающее сравнение. Идет постоянный итерационный процесс самовоспроизводства на основе очень простой рекуррентной формулы: Zn+1=(Zn)*(Zn)+C, где С – это некий коэффициент.

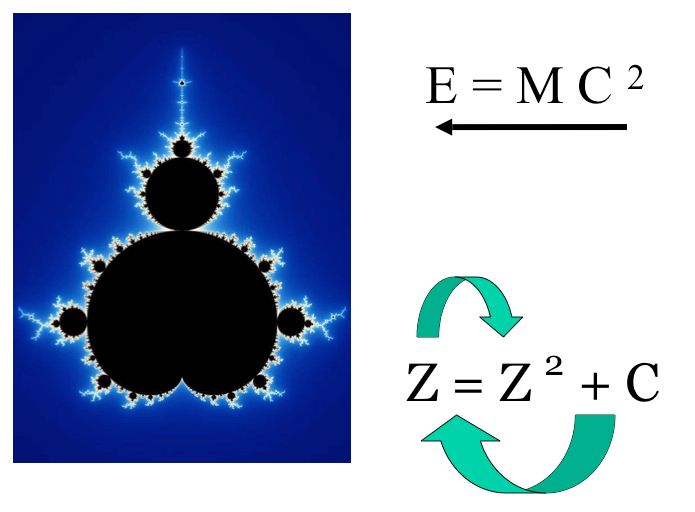
Термин «фрактал» был введен относительно недавно - в 1975 году - математиком Бенуа Мандельбротом, в честь которого и назван самый популярный фрактал.

Бенуа Мандельброт (1924-2010) французско - американский математик польского происхождения, родился в Варшаве в 1924 году в семье литовских евреев – его мать была врачом, отец - галантерейщиком. Лауреат премии Вольфа по физике (1993). В 1936 году вся семья эмигрировала во Францию и поселилась в Париже. Здесь Мандельброт попал под влияние своего дяди Шолема Мандельбройта, известного парижского математика, члена группы математиков, известной под общим псевдонимом Николя Бурбаки. У Бенуа Мандельброта открылся необычный математический дар - великолепное пространственное воображение - который позволил ему сразу после войны стать студентом Политехнической школы Парижа. Даже алгебраические задачи он решал геометрическим способом. Окончив университет, Мандельброт переехал в США, где окончил Калифорнийский технологический институт. В 1958 году Мандельброт окончательно поселился в США, где приступил к работе в научном центре IBM в Йорктауне, поскольку IBM в то время занималась интересными Бенуа Мандельброту областями математики. Он работал в области лингвистики, теории игр, экономики, аэронавтики, географии, физиологии, астрономии, физики вместе со знаменитым математиком фон Нейманом. Используя находящиеся в его распоряжении компьютеры IBM, Мандельброт создал графические изображения, сформированные на основе множества Мандельброта. По словам математика, он не чувствовал себя изобретателем, несмотря на то, что никто до него не создавал ничего подобного.

Но вернемся к нашему миру: все скопления, галактики, звезды и планеты, в какой бы части Вселенной они не находились, очень похожи между собой, но все же уникальны. Какая математическая структура обладает такими свойствами? Это фрактал.

А что это такое? - определение из интернета: «Фрактал — множество, обладающее свойством самоподобия». Или другими словами, фрактал – это фигура, которая строится за счет многократного повторения. Математики называют этот процесс "итерацией". Вот, к примеру, 10 наиболее популярных фракталов:

Фрактал порождается простейшей рекуррентной формулой, но развивается в красивейшую циклическую картину, каждый маленький кусочек которой одновременно и уникален, и похож на общую структуру. Самыми популярными фракталами являются описываемые множествами Джулия и Мандельброта. Причем фрактал Джулия описывается той же самой формулой, что и фрактал Мандельброта – но в них отличаются только значения коэффициента С. 

Несмотря на то, что природа очень самобытна и нелинейна, но она состоит из подобных элементов. Возьмем самый распространенный пример фрактала в природе — дерево. Оно состоит из подобных элементов: меленькая веточка подобна ветке крупнее и т.д. Так же выглядит русло реки, так же выглядит коннектор мозга, также выглядит карта интернета, кровеносная система, и т.д.

Асимметрия времени и вычисление рекуррентной функции

Кстати, как раз фрактальная структура нашей Вселенной открывает нам глаза на самую главную загадку современной физики — время. Идет ли время только вперед? Линейно ли оно?

Современная физика говорит о существовании так называемой асимметрии времени или стрел времени. Первая стрела времени — психологическая: мы помним прошлое, но не будущее. Эта асимметрия является частным случаем более общей второй стрелы времени — причинно-следственной. Причины порождают следствия, но не наоборот. С другой стороны это может быть лишь частью нашего восприятия, и при обратном ходе времени мы бы приняли причины за следствия, а следствия за причины. Но существует третья абсолютно объективная асимметрия времени, также называемая вторым законом термодинамики — энтропия в замкнутой системе со временем всегда растет***. То есть, при обратном ходе времени она бы падала.

***Примечание: вообще-то 2-й закон термодинамики противоречит закону эволюции!! Согласно закону эволюции, организмы по стреле времени усложняются. А закон гласит, что со временем все разрушается и наступает хаос. Так что, либо закон неправильный, либо система не замкнутая!

Как это можно объяснить? Одним из первых объяснение, согласующееся с гипотезой математической Вселенной, дал немецкий пионер компьютеро-строения и автор первого языка программирования высокого уровня Конрад Цузе. Он предположил, что наша Вселенная является не статичной математической моделью, а постоянно вычисляющейся чистой рекурсивной функцией. На вход такой функции поступает результат вычисления предыдущей итерации (прим.: это ж прям - самообучающаяся система, нейросеть)! Каждый тик такой функции является планковским временем, а, проще говоря, мгновением. Такая гипотеза очень хорошо объясняет все стрелы времени. Результат вычисления такой функции зависит от ее входа — будущее зависит от прошлого, но не наоборот. Со временем количество информации в такой системе будет расти, а, значит, будет расти и энтропия. И главное, эта гипотеза очень хорошо согласуется с фрактальностью нашей Вселенной, ведь фрактал — результат вычисления рекуррентной (рекурсивной) функции.

Таким образом, мы можем дать определение времени: время — это процесс вычисления чистой рекурсивной функции расчета развития нашей Вселенной. Также стоит учесть, что это время — не то же самое, что описывается в общей теории относительности Эйнштейна. Это абсолютное время — тики процессора, вычисляющего нашу Вселенную.

Матрица и антропный принцип по Тегмарку

Но если вся наша Вселенная — это вычислительная машина, то, как определить, что мы живем не в «Матрице»? С одной стороны это недоказуемо и неопровергаемо (фифти-на-фифти, т.е. – не знаю). С другой стороны, если мы живем в «Матрице», и крутимся на компе у какого-то программиста из реальной Вселенной, то его Вселенная тоже будет подчиняться законам математики и тоже может оказаться матрицей второго уровня, которая существует в реальном мире. Этот ряд можно продолжать до бесконечности и ни в одном уровне Матрицы не будет возможности доказать, существует или нет реальный мир более высокого уровня.

В любом случае, у Макса Тегмарка есть более красивое объяснение математичности нашей Вселенной. Для начала зададимся вопросом: почему мы живем именно в такой математической структуре, а не в какой-то другой? Тегмарк находит ответ на этот вопрос в антропном принципе «методом от противного»: все непротиворечивые математические структуры существуют, но лишь в немногих из них может зародиться такая тонко настроенная Вселенная, которая позволяет существовать нейронным сетям, способным осознавать причинно-следственные связи.

Земля песчинкою летит                                                                                            В потоке вечном мирозданья.                                                                                 В восторг приводит неба вид                                                                                 И этой бездны осознанье!                                                                        Мерцают мириады звёзд,                                                                                  Меж них туманности, планеты                                                                          И звёздный ветер вдаль несёт                                                                    Шлейф пролетающей кометы.                                                              Созвездий триллионы квант                                                                      Огнями манят снова, снова…                                                                            Вот вспыхнул красный сверхгигант                                                                  И, умер, став звездою новой.                                                                      Зрачки далёких чёрных дыр                                                                                 На нас, людей, взирают строго.                                                                Неужто, видя звёздный мир,                                                                  Возможна мысль, что нету Бога?                                                                  Игорь Морозов

«Я щаз один умный вещь скажу – только ты не абижайся, ладно?» (с) - «Вы можете возразить, что наша Вселенная недетерминирована и при коллапсе волновой функции Шредингера результат выхода кванта из суперпозиции непредсказуем. Но согласно многомировой интерпретации квантовой механики Эверетта в момент коллапса волновой функции наша Вселенная просто разделяется на две параллельных реальности, в одной из которых суперпозиция переходит в одно состояние, а в другой в противоположное». О!!!...ну кто-то и залепил… мозги всмятку))! Непонятно? - проще посмотреть ролик:

Фракталы в природе

Фракталы в анатомии

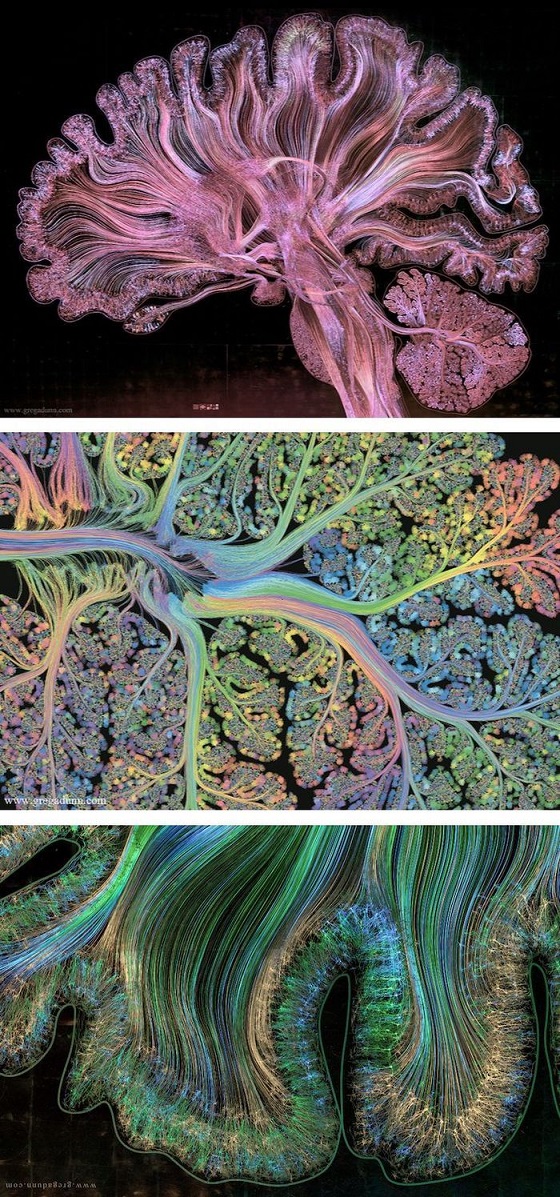
P.S.: В дополнение, кому интересно (!)– еще одно простое пояснение доктора физико-математических наук, профессора Свиридова В.В.

Использованы материалы:

https://topwar.ru/77676-velikiy-russkiy-geometr-nikolay-ivanovich-lobachevskiy.html

https://habr.com/ru/articles/517888/

https://smart-lab.ru/blog/852431.php

Еще материалы в блоге: https://cont.ws/@Nata_Urieva