Мир вокруг нас состоит из форм. Каждое существо или предмет, с которым мы взаимодействуем тем или иным образом, имеет форму. Тем не менее, форма – одна из вещей, которые мы часто игнорируем. Готовы поспорить, что многие люди даже не знают названия формы своего глаза. Таким образом, мы решили посвятить данную статью десяти интересным фактам о формах и фигурах, которые расширят ваш кругозор.
10. Мы открыли новую форму
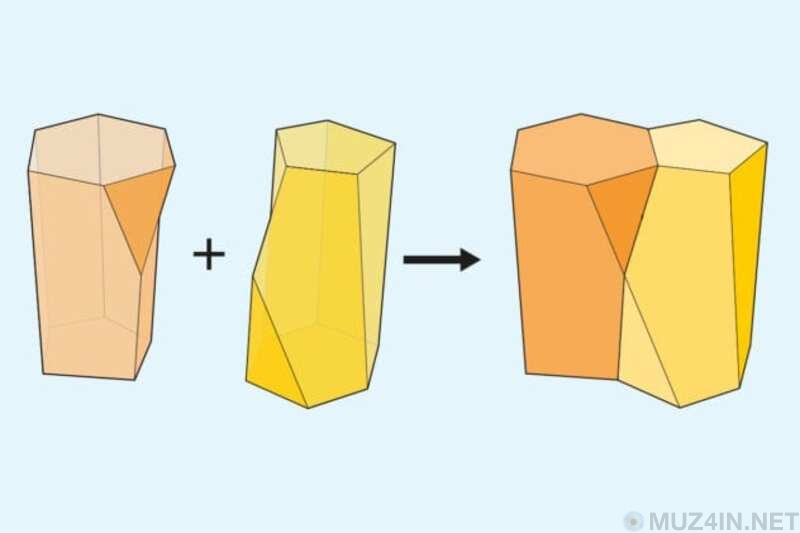
Открытие новой формы - это то, что происходит крайне редко. Однако 27 июля 2018 года учёные сообщили об открытии новой формы, названной скутоидом.
Скутоид представляет собой неправильную восьмигранную трёхмерную форму, которую мы можем лучше всего описать с помощью семигранной пятиугольной призмы.
Пятиугольная призма имеет семь граней – это верхушка и основание пятиугольника с пятью прямоугольными сторонами. Теперь представьте себе, что верхушка пятиугольника была отрезана таким образом, что он стал шестигранным шестиугольником. Этот разрез распространяется на часть двух соседних прямоугольных граней, создавая новую маленькую треугольную грань. Это скутоид.
Скутоиды можно найти в изогнутых частях человеческих органов. Эпителиальные клетки принимают форму скутоида, чтобы оставаться стабильными и экономить энергию. Любопытно, что эти клетки в других частях органов и тела выглядят как призмы и точки опоры.
9. Мы изобрели новую форму
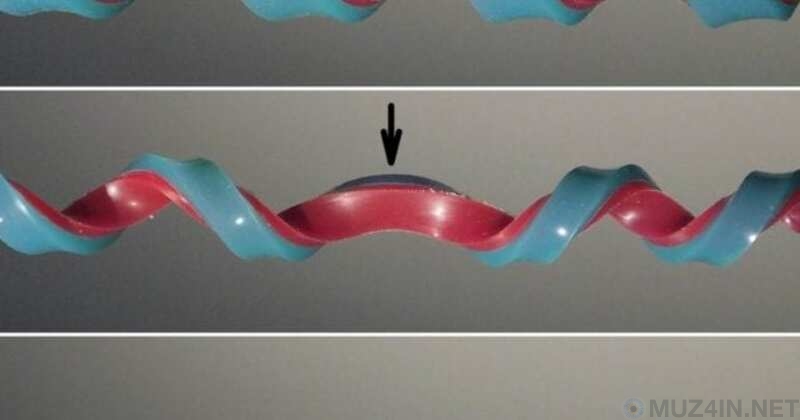
Когда учёные не открывают новые формы, они их изобретают. В данном пункте речь пойдёт о полуспирали, новой форме, изобретённой гарвардскими учёными. Они создали эту форму случайно, пытаясь сделать спиралевидные резиновые пружины для другого проекта.
Полуспираль тесно связана со спиралью. Вы наверняка знаете, как выглядят пружины, телефонные шнуры и изогнутые лестницы. Все они имеют форму спирали.
Вы можете легко создать полуспираль из гибких материалов, таких как телефонный шнур. Вам нужно крутить шнур до тех пор, пока часть его не станет длиннее других. Остальная часть спирали примет чрезвычайно изогнутую и более длинную форму, если вы продолжите скручивание, позволив вам получить полуспираль.
8. Кусочки пиццы – это не треугольники

Если бы вам нужно было выбрать всего один предмет для изучения фигур, пицца стала бы идеальным вариантом. Её выпекают кругом, нарезают треугольниками и доставляют в квадратных коробках. Но на самом деле всё гораздо сложнее.
Видите ли, пицца круглая, потому что это самый простой способ превратить тесто в пиццу. Её доставляют в квадратных коробках, потому что это самый простой способ транспортировать круглый объект. Однако пиццу разрезают не треугольниками, а секторами.
Сектор – это часть круга, которая берёт начало в центре и заканчивается любой точкой окружности (кривая линия круга). Кусок пиццы был бы треугольником, если бы все стороны были прямыми. Однако это круговой сектор, потому что две стороны прямые, а третья изогнутая.
7. Бумага – это не прямоугольник

Если вы спросите у любого человека, какую форму имеет лист бумаги, он ответит, что прямоугольную. Но так ли это на самом деле? Ответ – нет, и сейчас объясним почему.
Формы делятся на двумерные (2D) и трёхмерные (3D). Двумерные формы имеют длину и ширину, а трёхмерные – длину, ширину и толщину (высоту).
Фигуры, которые мы рисуем на бумаге, двумерные, поскольку у них есть только длина и ширина, хотя они могли бы выглядеть как трёхмерные, если бы мы добавили линии и тени. Тем не менее, всё, что нас окружает в повседневной жизни, имеет трёхмерную форму, включая бумагу, на которой мы рисуем.
Так почему же многие люди думают, что бумага имеет 2D-форму? Ответ кроется в главном различии между двумерными и трёхмерными формами. Первые всегда плоские, а вторые имеют толщину. Большинство людей думают, что бумага плоская, хотя на самом деле у неё есть толщина – небольшая и едва заметная, но она есть.
Итак, какой же 3D-формой обладает бумага? Прямоугольного параллелепипеда. Это трёхмерный эквивалент прямоугольника.
6. Фигуры, похожие на круги
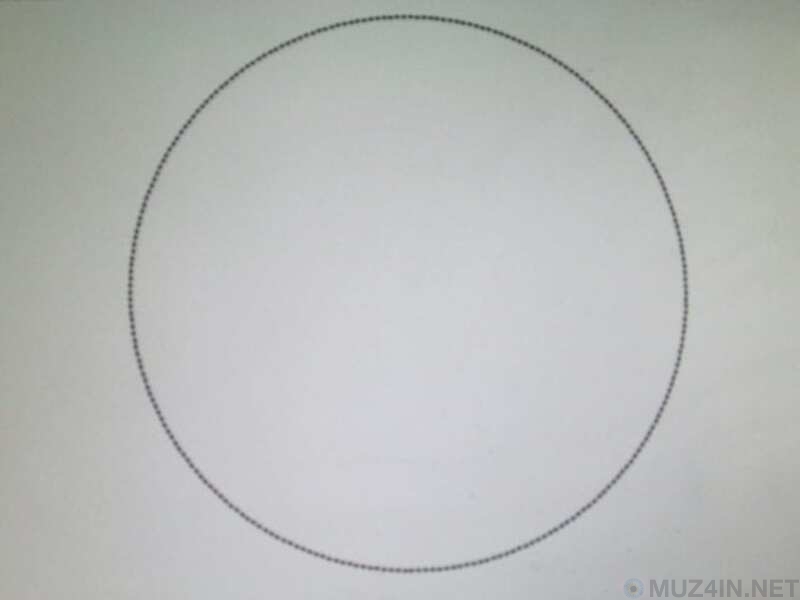
Если бы вас попросили назвать любую идеально круглую двумерную фигуру, вы бы ответили, что это круг, не так ли? Круг, очевидно, является единственной идеально круглой 2D-фигурой.
Очень жаль разочаровывать вас, но это не так. Есть ещё несколько 2D-фигур, которые обладают такой же идеальной формой, как и круг. На самом деле эти фигуры настолько похожи на круги, что их невозможно отличить друг от друга.
Правильный 257-угольник – одна из таких фигур. Это многоугольник с 257 сторонами. Многоугольник – это фигура, имеющая, по меньшей мере, три стороны с одинаковой длиной и углом. Равносторонний треугольник – это трёхгранный многоугольник, квадрат – четырёхгранный многоугольник, пятиугольник – пятигранный многоугольник, и так далее.
Тем не менее, правильный 257-угольник – не единственный конкурент круга. Правильный 65537-угольник – ещё один. Это многоугольник с 65537 сторонами.
5. Точки – это круги

Согласно логике, набор точек и линий может считаться фигурой лишь в том случае, если они создают форму, то есть они должны соприкасаться друг с другом, чтобы образовывать замкнутое пространство. Это означает, что точка или линия не являются фигурами, а трёхлинейная фигура (треугольник) является самой простой.
Что, если мы скажем вам, что точка – это фигура, в частности круг? Вы бы поверили? Что ж, это так, но чтобы понять, почему точка – это круг, нам сначала нужно понять, почему круг – это «круг».
Видите ли, круги не вписываются в общепринятое определение фигур. Хотя у них есть форма, грани и (изогнутая) линия, у них нет сторон. Они не имеют ни длины, ни ширины, но у них есть радиус, любая линия, идущая от центра к какой-то точке изогнутой линии.
Итак, какой наименьший возможный радиус может иметь круг? Ноль сантиметров. Если бы мы нарисовали круг радиусом в ноль сантиметров, это получилась бы точка. Как назвать эту точку? Очевидно, что кругом.
Математики на самом деле называют эту точку «вырожденным кругом».
4. Сфер не существует
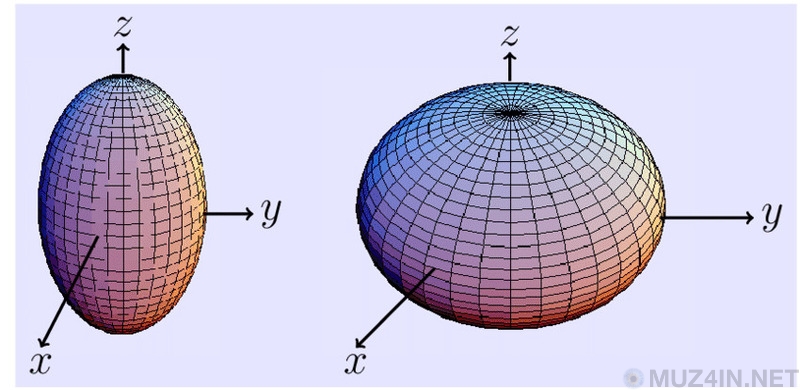
Среди математиков ведётся постоянный спор о том, существуют ли сферы в природе. Вы, вероятно, думаете, что сферы определённо существуют. Или планеты, луны и звёзды больше не сферические?
Чтобы ответить на этот вопрос, нам сначала нужно дать определение сфере. Объект считается сферой, если расстояние между его центром и кривой поверхностью всегда одинаково. Всегда ли одинаково расстояние между центром и кривой поверхностью любой планеты, звезды или луны? Нет.
Из-за скорости вращения и воздействия внутренних/внешних сил, все планеты, звёзды и луны более плоские у полюсов и шире у экваторов. Таким образом, расстояние между центром и кривой поверхностью больше по бокам и короче в верхней и нижней частях.
Это означает, что они не являются сферами. Так какой же они формы? Это сплюснутые сфероиды. Они выглядят как сферы, но не являются таковыми.
3. Квадратокруги – это не закруглённые квадраты

Возможно, вы никогда не слышали о квадратокругах, но вы стопроцентно их видели и принимали за квадраты. Квадратокруги – это гибрид квадратов и кругов. По сути, это квадраты с закруглёнными краями.
Однако квадратокруг – это не то же самое, что закруглённый квадрат, схожая фигура с аналогичным образом закруглёнными краями. Закруглённый квадрат сохраняет часть квадратных краёв.
Между тем, у квадратокругов края гладкие и округлые. Компания Apple часто использует квадратокруги в дизайне, и это одна из причин, почему её продукты обладают приятным визуалом.
2. Треугольные шины – это реальность

Вы когда-нибудь пробовали водить машину с квадратными колёсами? Когда-то это попытались сделать «Разрушители легенд», и опыт оказался не совсем комфортным как для водителя, так и для транспортного средства. Есть причина, почему шины и колёса круглые.
Однако можно ли сделать форму колёс и шин, отличную от круга? Да, мы можем сделать их из треугольников Рёло. Треугольник Рёло выглядит как треугольник, за исключением того, что его стороны изогнуты, а не прямые.
Чтобы создать его, начните с равностороннего треугольника. Затем нарисуйте три круга одинакового радиуса от каждого из трёх углов треугольника. Треугольник и три круглых сегмента, расположенных прямо за его сторонами, образуют треугольник Рёло.
Треугольник Рёло выступает в роли круга там, где круг не работает, или когда вам нужно что-то более эргономичное, чем круги. Например, если вы хотите сделать ротор, функционирующий в ограниченном пространстве (допустим, квадрат), вам нужно использовать треугольник Рёло, а не круг.
Треугольники Рёло также идеально подходят для изготовления современных карандашей, так как они обеспечивают лучшее сцепление. Они также могут быть использованы для изготовления колёс и шин для велосипедов и, возможно, даже автомобилей. Вы можете заменить круглые велосипедные колёса на те, что выполнены в форме треугольника Рёло, и они будут функционировать идеально, с небольшими изменениями, конечно же.
1. 4D-формы странные

Мы знакомы с 2D-формами, такими как квадраты, и 3D-формами, такими как кубы, но как насчёт 4D-форм, таких как тессеракты?
Чтобы понять, как выглядит тессеракт, представьте себе куб с шестью квадратными гранями. А теперь допустите, что каждая из шести граней является кубом сама по себе. Это и есть тессеракт.
4D-формы, подобные тессерактам, не существуют и являются лишь плодом воображения учёных. Однако неясно, смогли бы мы вообще их воспринимать, даже если бы они были реальными. Но кто знает? Если мы можем воспринимать несуществующие 2D-формы, то, возможно, мы смогли бы видеть и 4D-формы. Но, опять же, кто знает?
- Источник






Оценили 5 человек
6 кармы