Про параллельные прямые в Эвклидовой геометрии и геометрии Лобачевского. В чом отличие. Про параллельные линии в Сферометрии (часть Кривометрии) Грибов. Доказательство, что в Сферометрии все параллельные линии могут пересекаться.

Издавна *гео метрия* считалась средоточием незыблемых истин и безукоризненных суждений.  Свыше двух тысяч лет умами владела, да и нуне владеет геометрия Эвклида.  В этой геометрии есть так называемый *пятый постулат о параллельных* :  /*/ И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых /*/.  Этот *пятый постулат*, почему-то, не представлялся некоторым умствующим субъектам столь очевидным, как другие постулаты Эвклида, и они упорно пытались доказать его. Вот неполный список этих субъектов, которые умственно типа трудились над этой высосанной из пальца проблемой: Аристотель, Птолемей, Прокл, Лейбниц, Декарт, Ампер, Ла-гранж, Фурье, Бертран, Якоби.

Что до Нас,  то Мы щитаем, что *пятый постулат* Эвклида не порождает никаких непоняток. Достаточно не то што в уме, а на плоском чём-нибуть нарисовать две непараллельные линии, а потом продолжыть их в ту сторону, где предполагается, что они сойдутся. И вскоре можно воочию убедиться, глазьями своими увидеть, разглядеть в объективно существующей *реальности*, как пересекутся эти не параллельные сходящиеся линии. Ну куда уж убедительнее. Можно даже микроскоп взять и разглядеть как эти линии пересеклись.   

Вот и русский ученый, профессор Казанского университета Николай Иванович Лобачевский зачем-то создал новую геометрическую систему, которую он сам назвал "воображаемой". 

После длительных умственных поисков непонятно чего  Лобачевский вдруг обнаружил вот чего:  он умственным взором углядел, что помимо геометрии Эвклида, описывающей *реальность*,  внутри его головы, будто бы,  существует ещо и другая геометрия, построенная на отрицании *пятого постулата* Эвклида.  Лобачевский подподумал, да и назвал эту геометрию, летающую у него в голове пред его умственным взором , *воображаемой геометрией*.

В архивах сохранился документ - сопроводительная записка Лобачевского к докладу, которая начинается словами: "Препровождаю сочинение мое под названием "Сжатое изложение начал геометрии о параллельных линиях". Желаю знать мнение о сем ученых, моих сотоварищей". На документе указана дата - "7-го февраля 1826 г.", внизу - "Слушано 1826 г. 11 февраля". Итак, 11 февраля 1826 г. в Казани впервые  было публично доложено об обнаружении Лобачевским внутри своей головы некой *воображаемой геометрии*, получившей название неэвклидовой.

Разница меж Эвклидовой геометрией и *воображаемой геометрией* Лобачевского.

В *воображаемой геометрии* (то есть в не связанной с *реальностью* геометрии) Лобачевского можно вот чего:   «через точку, не лежащую на заданной прямой, можно провести более одной прямой, параллельной этой заданной прямой». Почему нет? Пространство-то воображаемое. Чо хош, то и воображай...

А в Эвклидовой геометрии, отражающей объективную *реальность* — «через точку, не лежащую на заданной прямой, можно провести только одну прямую, параллельной этой заданной прямой» . Да. Как ни старайся, скока ни черти, новая параллельная линия всегда будет накладываться на предыдущую параллельную линию и будет всё это выглядеть как одна линия. 

Вот и вся разница.

Теперь поговорим о Сферометрии Грибов  как о неотъемлемой части учения под названьем  Кривометрия Грибов. 

В чом же конкретно состоит отличие названной Сферометрии  от геометрии Эвклида (Плоскометрия) и *воображаемой геометрии* Лобачевского (произвольных фантазий, не связанных с *реальностью*)?   Отличие не вообще, а лишь в той части этих гео метрий, которые касаются параллельных прямых. 

Во-первых, названная Сферометрия относится к учению Кривометрия Грибов, а геометрия Эвклида есть часть многовекового учения человецей под названием  Плоскометрия .

Плоскометрия  как многовековое учение человецей объединяет в себе всё умное, что придумано в веках учоными человецыками про плоские точки, плоские прямые линии, плоские плоскости в двухмерном (2Д) пространстве.  Плоскостопием, если у кого-то возникнет такой вопрос, сие учение не интересуется.

Кривометрия как учение Грибов объединяет в себе всё умное, что касается шарообразных точек и цылиндрических кривых линий, криволинейных плоскостей, объёмов меж криволинейными и плоскими  плоскостями в трёхмерном (3Д) пространстве. Кривоумия и криворукости, если у кого возникнет такой вопрос, сие учение не касается.

Во-вторых, Сферометрия Грибов отражает объективно существующую *реальность* (посмотрите на сферы, окружающие Вас в *реальности*), что роднит её с Эфклидовой геометрией, тогда как *воображаемая геометрия*  Лобачевского являет собой вольный изврат  Эвклидовой геометрии, никак не связанный с *реальностью*.  

Теперь, кое как сориентировавшысь в трёх науках - в Эвклидовой геометрии, в *воображаемой геометрии* Лобачевского и в Сферометрии Грибов, давайте ка посмотрим на то, какие свойства имеют параллельные линии на поверхности сферы.

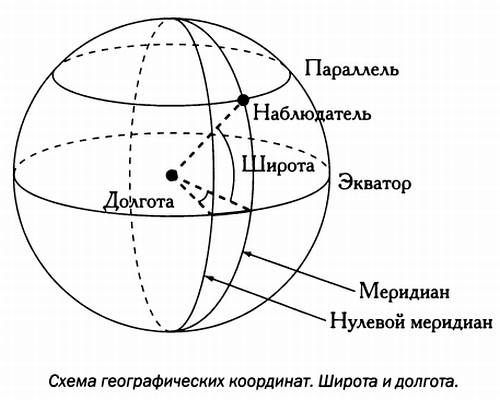
*Меридианы* на сфере  видите? Хорошо.

Верите ли, что в любых точках пересечения *мередианов* с *экватором* угол между линией *экватора* и линией *меридиана* всегда равен 90 градусам (т.н. *прямой угол*).

Вполне очевидно, что если все меридианы перпендикулярны *экватору*, то все они, одновременно, параллельны друг другу.

В Плоскометрии есть даже спецыальная система отображения этого обстоятельства для глобуса Земли. Смотрите:

  

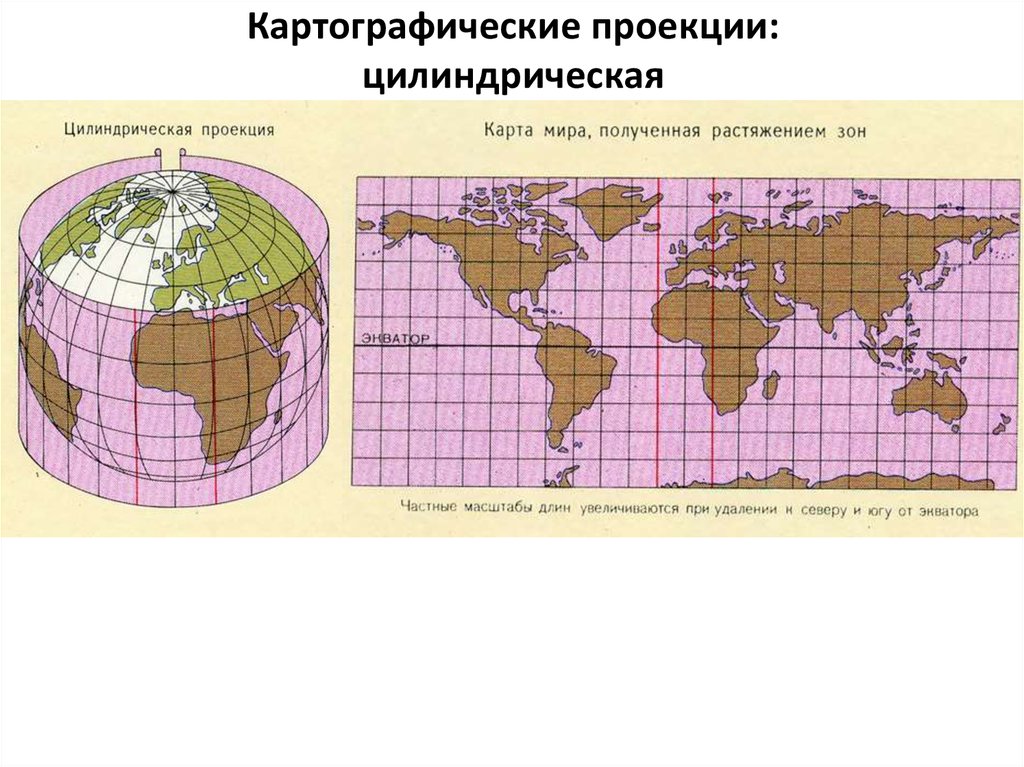
Все *мередианы* параллельны друг другу и, скока их не продолжай в абстрактной цылиндрической картографической проекцыи , параллельные меридианы  никогда не пересекутся.

Иначе происходит в Сферометрии. Параллельные линии в Сферометрии, если они параллельны оси вращения сферы, всегда пересекаются. Точка их пересечения именуется *полюсом*.  На примеге Глобуса Земли невооружонным взглядом видно, что таких полюсов у сферы два штуки. В этих полюсах и пересекаются все без исключения параллельные *мередианы*. Как ни крути.

Нужно ли это доказывать, или это постулат, аналогичный *пятому постулату* Эвклида, только в Сферометрии (Учения Кривометрия), а не в Эвклидовой геометрии (Учения Плоскометрия)?

Это, однозначно, постулат, ибо пересечение параллельных линий на сфере настолько очевидно, что не требует доказательств.

Поздравляем.

Сёдня Вы стали свидетелями события, равного по научному значению слушано 11 февраля 1826 г. "Сжатого изложения начал геометрии о параллельных линиях" Лобачевского, положывшего начало так называемой неэвклидовой геометрии.

Сёдня, 11 Июля 2020 Грибами положено одно из начал Сферометрии (часть Кривометрии) о параллельных линиях. Сферометрия является,  одновременно, и неэвклидовой, и нелобачевской. Это самостоятельное  направление в Кривометрии.

.

Грибы.