Теория относительности довольно сложна для интуитивного восприятия, и неудивительно, что многие её выводы выглядят весьма и весьма парадоксально. Сегодня мы рассмотрим один известный парадокс, который многие совершенно необоснованно считают противоречием, доказывающим несостоятельность самой теории.
Для того, чтобы понимать матчасть, настоятельно советую ознакомиться с предыдущей статьёй.
Постановка проблемы
Как известно, в соответствии с теорией относительности время в каждой системе отсчёта течёт по-своему, согласование течения времени между разными СО может быть весьма непростым и неочевидным делом. В парадоксе близнецов, при всей его кажущейся простоте, это проявляется весьма ярко.
Представим себе двух близнецов с планеты A, один из которых отправляется в полёт на планету B, затем возвращается. Время близнеца-путешественника с точки зрения близнеца-домоседа замедляется, и в момент возвращения ожидается, что его часы будут показывать меньшее время. Однако если рассмотреть ситуацию с точки зрения путешественника, то как раз домосед движется, и его часы должны показывать меньше времени, чем часы путешественника. Ой, кажется, мы нашли противоречие?
Вот как выглядит полёт с точки зрения каждого из близнецов:

Ниспровергатели очень любят парадокс близнецов, так как, по их мнению, он кардинально неразрешим в ТО. Мы скоро увидим, что это абсолютно не соответствует действительности, что противоречие тут мнимое, и вызвано оно недостаточно глубоким пониманием теории. Заодно мы научимся лучше понимать саму суть тезиса "всё относительно".
Геометрия парадокса
В СТО нет времени как чего-то абсолютного и неизменного, ход времени в каждой ИСО свой, и это надо учитывать при строгом и внимательном рассмотрении любого процесса.
Рассмотрим ситуацию парадокса в виде геометрических графиков в пространстве-времени Минковского:

Тут изображена ситуация с точки зрения домоседа (Б1), систему отсчёта которого мы будем считать инерциальной. Его мировая линия совпадает с осью времени, а мировая линия путешественника (Б2) представляет из себя ломаную линию.
Система отсчёта домоседа Б1 является ИСО, но в то же время СО путешественника Б2 не является ИСО. В самом деле, в этом случае его мировая линия должна быть прямой в любой другой ИСО, а не ломанной. В то же время в каждой из половин пути (их я раскрасил в синий и зелёный цвета) СО Б2 является ИСО. Рассмотрим, например, ситуацию с точки зрения ИСО первой половины пути:
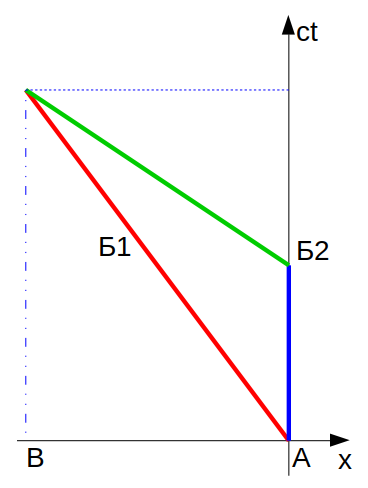
С точки зрения "синей" ИСО домосед Б1 удаляется со скоростью v, а Б2 сначала никуда не движется, а потом начинает догонять Б1 с "двойной" релятивистской скоростью 2v/(1+v^2/c^2).
Как нетрудно видеть, мировая линия Б2 в обоих случаях является ломаной. Более того, она будет ломаной вообще в любой ИСО, поскольку СО Б2 не является инерциальной.
Вот тут и скрывается разгадка парадокса: нет, точки зрения близнецов несимметричны, один из них существует в НСО ("сине-зелёной"). Так у кого же из близнецов будет короче борода в момент встречи?
Мы привыкли к тому, что кратчайшим расстоянием между точками всегда является расстояние по прямой. Но это справедливо для евклидовых пространств, а у нас пространство псевдоевклидово, в нём время участвует со знаком "минус". Это приводит к неожиданному эффекту: чем длиннее мировая линия между двумя событиями, тем меньшее собственное время ей соответствует. Поэтому часы путешественника насчитают строго меньше, чем часы домоседа. Это и будет правильный ответ.
Странно, да? Но сейчас мы разберёмся во всём этом подробнее и увидим, что ничего странного нет, что всё на самом деле очень логично и чётко.
Всё дело в ускорении?
Есть вопиюще неверное объяснение парадокса, которое заключается в том, что время путешественника сокращается за счёт ускорения, нужного для старта, финиша и разворота (мы всем этим пренебрегли для упрощения). Я не знаю, почему эта идея так популярна, но даже бедная несчастная Википедия в статье о парадоксе не избежала этого мифа. На самом деле модель мысленного эксперимента можно изменить таким образом, что никакого ускорения в нём не будет, а вот сокращение времени всё равно останется и никуда не денется! Потому что дело тут совсем не в ускорении.
Вместо двух близнецов рассмотрим трёх: Б1, Б2 и Б3. Близнец Б1 находится на планете и никуда не движется. Близнец Б2 изначально движется с постоянной скоростью v (по инерции) и в момент пролетания мимо планеты A считывает у Б1 показания его часов. Близнец Б3 движется из глубины космоса со скоростью v таким образом, чтобы встретиться с Б2 в момент "разворота" у планеты B и считать показания его часов. Никакого "разворота" при этом не совершается, и обратный путь до Б1 вместо Б2 выполняет Б3. Все участники этого эксперимента живут уже в настоящих ИСО, никуда не ускоряются, независимо считают время и синхронизируют его строго в точках встречи.
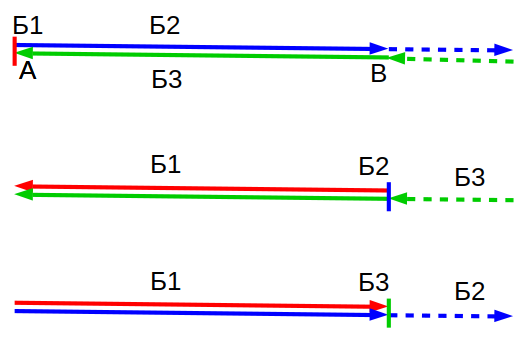
На этих схемах изображён взгляд каждого из наблюдателей на движение всех участников эксперимента.
С точки зрения Б1 от него улетает Б2 со скорость v, одновременно навстречу летит Б3 со скоростью v.
С точки зрения Б2 от него улетает Б1 со скоростью v, а навстречу летит Б3 с "двойной" скоростью 2v/(1+v^2/c^2).
С точки зрения Б3 к нему навстречу летят Б1 со скоростью v и Б2 со скоростью 2v/(1+v^2/c^2).
И сколько же натикают часы каждого из них? Из таких схем это абсолютно непонятно. Нужно рисовать и внимательно анализировать диаграммы Минковского.
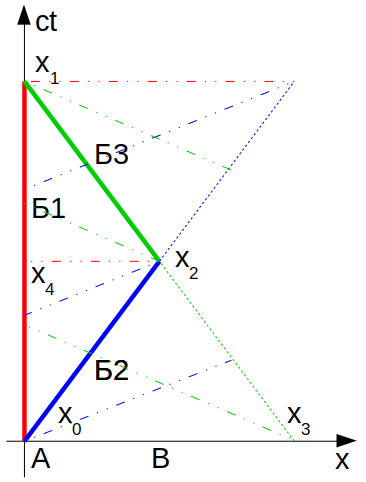
На этом графике пунктиром нарисованы линии одновременности для каждого из наблюдателей, а также отмечены некоторые точки. Общее время, которое насчитает Б2 до встречи с Б3, плюс время, которое насчитает Б3 от момента встречи с Б2 до момента встречи с Б1, всё равно окажется меньше собственного времени Б1.
Почему же так? Ведь вроде бы Б3 летит с такой же скоростью, что и Б2, чем они отличаются? Дело в том, что ИСО у Б2 и Б3 совсем другие, чем у Б1. Например, точка x3 (которая, с точки зрения Б1, соответствует положению Б3 в момент старта Б2 с планеты), с точки зрения Б2 и Б3 не только не является одновременной с моментом x0, но даже последовательность этих событий различается! Так, Б3 считает, что x3 случается позже x0, а Б2 - что раньше.
Вот так выглядит ситуация с точки зрения Б2, тут отмечены те же самые точки x0...x4 для сравнения с предыдущим графиком:
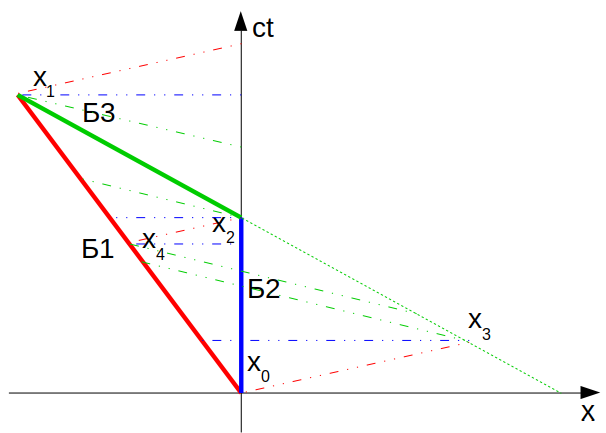
Зная представления каждого из близнецов об "одновременности", можно отметить их собственное время на шкале времени в одном масштабе с временем Б1:
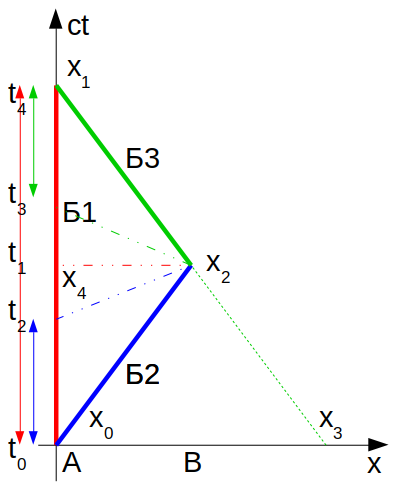
Путешественники в сумме насчитают меньше, чем домосед. Как и должно быть по теории. В самом деле, с учётом релятивистского сокращения времени ситуация будет следующей:
Близнец Б1 насчитает время t на отрезке x0-x1 (красная стрелка).
Близнец Б2 насчитает время t/2*sqrt(1-v^2/c^2) на отрезке x0-x2 (синяя стрелка).
Близнец Б3 насчитает время t/2*sqrt(1-v^2/c^2) на отрезке x2-x1 (зелёная стрелка).
В итоге Б1 насчитает t, а Б2+Б3 насчитают t*sqrt(1-v^2/c^2), что меньше t.
Вся парадоксальность нашего эксперимента сводится к тому, что по мнению Б2 в момент встречи с Б3 время составляет t2, а по мнению Б3 - t3, в то время как Б1 считает, что его время в момент их встречи t1. В итоге близнецы Б2 и Б3 из расчёта времени упускают участок между t2 и t3, вот и выходит меньше, чем у Б1.
Смена ИСО наблюдения не изменит это соотношение. Например, в "синей" ИСО Б2 ситуация выглядит следующим образом:

В общем, как ни крути, а путешественник Б2+Б3 насчитает времени меньше домоседа. Он просто посчитает время в других шкалах времени, чем Б1. И никакая смена ИСО наблюдения не поможет свести этот факт к противоречию.
Невозможность симметрии
Можно ли добиться симметрии в парадоксе близнецов, чтобы таки подвести противоречие под их взгляды друг на друга? Симметрия означает, что два близнеца движутся по инерции с одинаковой скоростью друг от друга, каждый наблюдает релятивистское сокращение времени на одинаковую величину, но в силу их полной идентичности никто из них не может насчитать времени меньше другого. Возможно ли такое? Давайте попробуем это представить.
Пусть есть два близнеца, и пусть СО каждого из них будет инерциальна. Тогда в любой ИСО мировые линии обоих близнецов будут прямыми. Как известно, две несовпадающие прямые могут пересекаться только в одной точке - и это будет точка старта полёта. Таким образом, близнецы после старта никогда больше не смогуть встретится и продемонстрировать "противоречивое" мнение своих часов.
Не получается противоречия, увы.
Обобщение на произвольный маршрут путешественника
С точки зрения неподвижного в данной ИСО наблюдателя мировая линия представляет из себя вертикальную ось времени, а линии одновременности горизонтальны. Если же мировая линия не вертикальна, то линии одновременности будут наклонены, и та же самая длина мировой линии будет соответствовать меньшей проекции на ось времени.
По сути это и есть геометрическая интерпретация сокращения времени. За счёт этого любая ломаная мировая линия будет создавать сумму релятивистски укороченных отрезков времени. Более длинная мировая линия создаёт сумму более коротких временных интервалов.
Кстати, аналогично наблюдается сокращение длины проекции на пространственную ось - это геометрическая интерпретация релятивистского сокращения расстояний.
Если вдруг мировая линия представляет из себя что-то более сложное, чем ломаная, то общий принцип всё равно сохраняется: из двух мировых линий между двумя событиями меньшее собственное время насчитает та, которая длиннее. В самом деле, можно приблизить произвольную кривую линию ломаной, состоящей из коротких отрезков. Чем меньше длина отрезков, тем точнее ломаная приближает кривую - в предельном переходе совпадая с ней. Таким образом, близнец-путешественник всегда получает сокращение времени, так как его мировая линия длиннее мировой линии домоседа.
В общем случае "парадокс близнецов" выражается как раз в неодинаковости "натикавшего" времени между двумя встречами близнецов, которые движутся в пространстве как угодно, если длины их мировых линий не совпадают.
Круговое движение близнецов
Рассмотрим систему двух близнецов Б2 и Б3, вращающихся вокруг неподвижной планеты по окружности радиуса R в противоположном направлении. И отдельно то же самое вокруг вращающейся планеты:
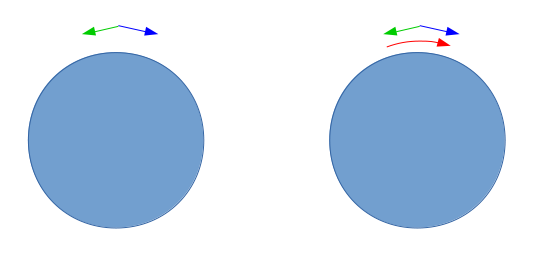
В случае неподвижной планеты мировые линии близнецов Б2 и Б3 будут представлять из себя "синусоиды" вокруг оси времени:
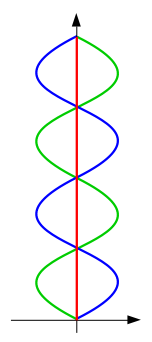
Каждый из близнецов насчитает меньше времени, чем неподвижный наблюдатель Б1 на поверхности планеты.
Примечание. На самом деле, конечно, мировые линии близнецов не являются никакими синусоидами, они будут представлять из себя спирали, закрученные вокруг оси времени в противоположных направлениях, а синусоидами будут только их проекции на отдельные координатные плоскости. Но общий принцип можно понять и на плоских графиках с синусоидами.
В случае вращающейся планеты "неподвижный" Б1 на самом деле не будет неподвижным - он тоже вращается. Теперь угловая скорость движения близнецов относительно ИСО неодинакова: в одну сторону она складывается с вращением планеты, а в другую - вычитается. Мировые линии тоже изменились:
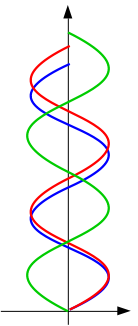
Тут видно, что время близнеца Б2 должно быть меньше времени "неподвижного" (относительно планеты) Б1, а время Б3, наоборот, больше.
Эксперимент Хафеле-Китинга
В 1970 году физик Джозеф Хафеле опубликовал в Nature статью, в которой предположил, что при движении на типичном самолёте можно достичь увеличения/уменьшения времени на величину порядка сотен наносекунд, совершив кругосветное путешествие, то есть без субсветовых скоростей и многолетних полётов в дальний космос можно проверить парадокс близнецов на практике. Условия для такого эксперимента не выглядели безумными, и уже в 1971 году Хафеле вместе с астрономом Ричардом Китингом, сотрудником Time Services Division U.S. Naval Observatory (для справки, эта обсерватория поставляет точное время для системы GPS) совершили два полёта на самолётах вокруг света вместе с атомными цезиевыми часами HP 5061A. Для часов были куплены два билета на имя Mr Clock :D На билеты для экспериментаторов и часов (4 места) было потрачено около 7600 долларов.

Хафеле, Китинг и атомные часы. А также стюардесса, которая демонстративно проверяет время по своим наручным часам. Фото из журнала Popular Mechanics, январь 1972 г.
Результат эксперимента Хафеле-Китинга показал, что цезиевые часы действительно насчитали разницу во времени по сравнению с "неподвижными" часами U.S. Naval Observatory. Эта разница близка к рассчитанным по СТО (кинематические эффекты) и ОТО (гравитационные эффекты) значениям (в наносекундах):
На запад: эффекты ОТО: +179 ±18, эффекты СТО: +96±10, сумма: +275±21, результат фактических измерений: +273±7
На восток: эффекты ОТО: +144±14, эффекты СТО: −184±18, сумма: −40±23, результат фактических измерений: −59±10.
До сих пор мы рассматривали парадокс близнецов только с точки зрения СТО, однако ОТО за счёт гравитационного поля планеты добавляет дополнительных искажений к ходу времени.
Эксперимент Хафеле-Китинга практически продемонстрировал реальность изменения времени, которое ожидалось в парадоксе близнецов.
Ссылки на статьи об эксперименте:
J. C. Hafele. Relativistic Behaviour of Moving Terrestrial Clocks // Nature volume 227 (July 18, 1970)
J. C. Hafele. Performance and Results of Portable Clocks in Aircraft // PTTI 3d Annual Meeting (November 16-18, 1971)
J. C. Hafele, R. E. Keating. Around-the-World Atomic Clocks: Predicted Relativistic Time Gains // Science. Vol. 177 (4044) p. 166–168 (July 14, 1972)
J. C. Hafele, R. E. Keating. Around-the-World Atomic Clocks: Observed Relativistic Time Gains // Science. Vol. 177 (4044) p. 168–170 (July 14, 1972)















Оценили 17 человек
37 кармы