Мауриц Эшер - безумство черно-белых линий.

Голландский художник Мауриц Корнелис Эшер, уникальный в своем роде график, чьи бредовые на первый взгляд картины выстроены по строгим законам логики и геометрии.

 Художник невозможных фигур

 Хотя Эшер не принадлежал к основному потоку авангардного искусства XX века, считается, что его творчество следует рассматривать в контексте теории относительности Эйнштейна, фрейдовского психоанализа, кубизма и прочих достижений в области соотношений пространства, времени и их тождественности.

Для сюжетов «классических» произведений Эшера («Рисующие руки», «Метаморфозы», «День и ночь», «Рептилии», «Встреча», «Дом с лестницей» и т. д.) характерно остроумное осмысление логических и пластических парадоксов. В сочетании с виртуозной техникой это производит сильнейшее впечатление.

Перспективные метаморфозы

Одним из самых выдающихся аспектов творчества Эшера является изображение «метаморфоз», фигурирующих в разных формах во множестве работ. Художник подробно исследует постепенность перехода от одной геометрической фигуры к другой, посредством незначительных изменений в очертаниях. Кроме того, Эшер неоднократно рисовал метаморфозы, происходящие с живыми существами (птицы превращаются у него в рыб и прочее) и даже «одушевлял» в ходе метаморфоз неодушевлённые предметы, превращая их в живые существа.

На множестве картин Эшера происходит демонстрация упорядоченного сечения плоскости или заполнение её тождественными формами, которые без зазоров, плотно, прилегают друг к другу (навеяно «мавританским» средневековым стилем).

Мозаики - из плоскости в обьем

Математически доказано, что регулярное замощение плоскости возможно только тремя правильными многоугольниками: треугольником, квадратом и шестиугольником. Эшер интересовался как регулярными мозаиками, так и нерегулярными. Кроме того, что художник использовал нерегулярные мозаики (образующие неповторяющиеся узоры), он много работал с метаморфозами, изменяя многоугольники под зооморфные формы, заполняющие поверхность. Интерес к мозаикам проявился в 1936 во время путешествия в Испании под влиянием геометрических орнаментов Альгамбры.

Художник не только интересовался нерегулярным заполнением плоскости, называя это игрой, он совмещал эксперименты с заполнением плоскости с экспериментами с переходами плоскости в объём и наоборот («Рептилии»).

Многогранники и непрямые прямые

Многогранники в работах Эшера играют роль как основной фигуры, так и вспомогательных элементов. В работах «Порядок и хаос» и «Звёзды» художник использует негеометрические формы для усиления впечатления от правильности центральных фигур: в первой из упомянутых работ в символе порядка и красоты отражается хаотическое собрание ненужных, сломанных, разбитых предметов, а во второй в конструкции из трёх правильных полых октаэдров живут два хамелеона.

Многоугольники, как и сферы, используются в работах Эшера для создания перспективы. Последней литографией в серии многоугольников была «Гравитация». На ней изображён додекаэдр, образованный двенадцатью плоскими пятиконечными звёздами. На каждой из площадок живёт длинношеее четырёхногое бесхвостое фантастическое животное; его туловище находится в пирамиде, в отверстия которой оно высовывает конечности, верхушка пирамиды является одной из стен жилища соседнего чудовища. Пирамиды одновременно выступают и как стены, и как полы: литография служит переходом к группе относительность.

Спирали как форма бытия

Основных видов спиралей, используемых Эшером в своих работах, можно назвать три: спирали-мозаики (например, гравюра «Водовороты», в которой художник работал над бесконечным множеством применительно к заполнению поверхности), образование поверхности (например, в гравюре «Сферические спирали» изображены 4 ленты, образующие сферическую поверхность, проходящие от полюса к полюсу, бесконечно малые на полюсах и широкие к экватору), закручивание спиралей самих в себя (работа «Спирали»).

Форма пространства - конфликт формы и содержимого

Эшера волновали особенности перехода от плоскости к пространству, взаимодействие имеющих определённую форму двухмерных фигур и трёхмерных существ, способных передвигаться в пространстве. Эшер стремился иллюстрировать динамику явления, и видел абсурд в том, что несколько проведённых линий могут восприниматься глазом как объёмная фигура.

Примером работы, в которой художник изучал такое восприятие — в работе «Три пересекающиеся плоскости», где каждая плоскость, составленная из квадратных плиток, расположенных в шахматном порядке, сокращается в перспективе до точки, три получившиеся точки образуют равносторонний треугольник.

Помимо этого, Эшер работал над заполнением пространства; на его взгляд, из созданных на эту тему работ идеальной по композиции может считаться третий «Предел круга» (рыбоподобные фигуры уменьшаются при удалении от центра круга, плотно заполняя при этом поверхность; подобное уменьшение может быть бесконечным; при этом картина демонстрирует один из видов неевклидова пространства, описанный Анри Пуанкаре: теоретически находящийся в этом пространстве человек не будет чувствовать ничего необычного, но не сможет нарисовать фигуры с четырьмя прямыми углами, соединёнными прямыми линиями, так как в этом пространстве не существует квадратов и прямоугольников).

Из известных работ, связанных с формой пространства, можно назвать также ленты Мёбиуса Эшера.

Логика пространства - все страньше и страньше...

В качестве картины, в которой исследуется и логика пространства, и его топология, можно назвать литографию «Выставка гравюр». Центральная часть пространства растянута, при этом оно изгибается по часовой стрелке вокруг незаполненного центра. Справа снизу вход; следуя взглядом по галерее, читатель выходит на левый нижний угол, в котором стоит юноша, по размерам раза в четыре больше первого. Юноша рассматривает пароход, изображённый на гравюре, которая идёт влево; на ней изображены лодки, канал, дома; из одного из окон выглядывает женщина, которая смотрит… на крышу галереи, в которой находится юноша.

Художник создавал на своих картинах оптические иллюзии, в основном с помощью светотени. Например, на картине «Куб с полосками» невозможно определить, в какую сторону обращены объёмные «пуговицы», расположенные на ленте.

Кроме того, «игрой» с логикой пространства являются картины Эшера, на которых изображены различные «невозможные фигуры»; Эшер изображал их как отдельно, так и в сюжетных литографиях и гравюрах, самой примечательной из которых является, вероятно, литография «Водопад», основанная на невозможном треугольнике (треугольник Пенроуза). Водопад играет роль вечного двигателя, а башни кажутся одинаковой высоты, хотя в каждой из них на этаж меньше, чем в соседней. Две другие гравюры Эшера с невозможными фигурами — «Бельведер» и «Спускаясь и поднимаясь». Все три созданы между 1958 и 1961 годами.

Эшер работает с проблемами перспективы, начиная с ранних гравюр («Вавилонская башня»); спустя десятилетия после её создания работа над перспективой велась уже не ради интересных ракурсов, но и для создания полуабсурдных произведений, позволяющих рассмотреть один и тот же объект с разных точек в рамках единой картины («Другой мир II», «Выше и ниже»). Например, на литографии «Выше и ниже» художник разместил сразу пять «точек исчезновения» (точек, которые «сообщают» глазу человека о бесконечности пространства.

Самовоспроизведение - руки превращааааются....

Наиболее полное исследование этого вопроса в творчестве художника освещено в книге Дугласа Хофштадтера «Гёдель, Эшер, Бах: эта бесконечная гирлянда (Gdel, Escher, Bach: An Eternal Golden Braid)», выпущенной в 1980 году и награждённой Пулитцеровской премией.

Наиболее очевидна тема самовоспроизведения в литографии «Рисующие руки»: хорошо прорисованы кисти рук, рисуют сами себя..

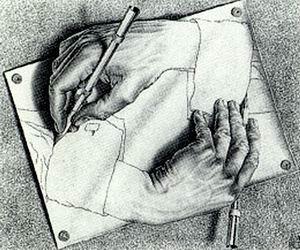
Никудышний математик

Работами Эшера иллюстрируют математические примеры, однако сам художник говорил что мало понимает в математике.Однажды известный геометр Г. Кокстер пригласил художника на свою лекцию, посвященную математическому содержанию его гравюр и литографий. К взаимному разочарованию, Морис Эшер не понял почти ни слова из того, о чем рассказывал Кокстер. Вот что писал об этом сам художник: «Я так ни разу и не смог получить хорошей оценки по математике. Забавно, что я неожиданно оказался связанным с этой наукой. Поверьте, в школе я был очень плохим учеником. И вот теперь математики используют мои рисунки для иллюстрации своих книг. Представьте себе, эти ученые люди принимают меня в свою компанию как потерянного и вновь обретенного брата! Они, кажется, не подозревают, что математически я абсолютно безграмотен».

Источник