Какой коэффициент полезного действия может быть у "египетского циркуля"?

В прошлой статье я дал возможный вариант передвижки трехтонных каменных блоков в условиях Древнего Египта.  Был ли такой вариант в реальности - вопрос открытый.  И термин "египетский циркуль" - условный. Но законы механики реальность такого циркуля допускают, а его ооочень примитивная конструкция дает нам право предположить, что она могла быть реализована в условиях Древнего Египта.

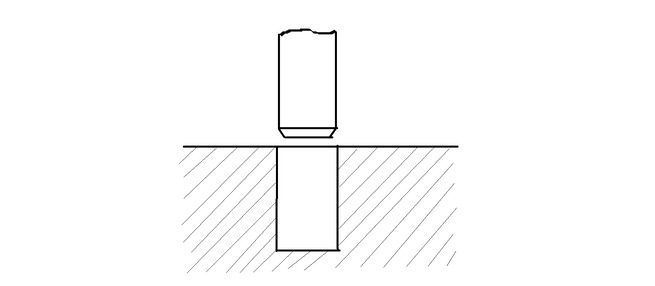
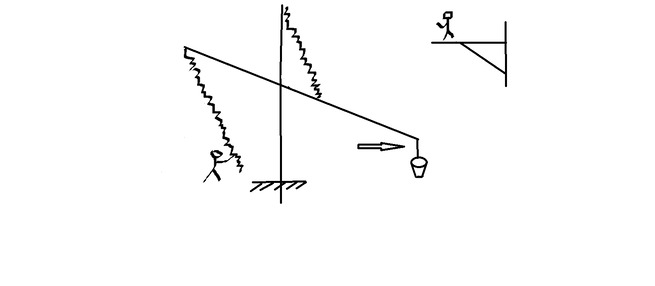
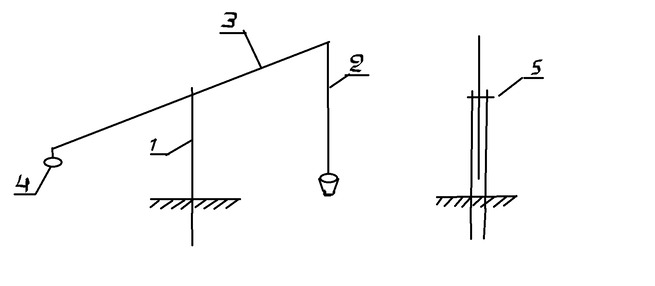
Напомню его конструкцию

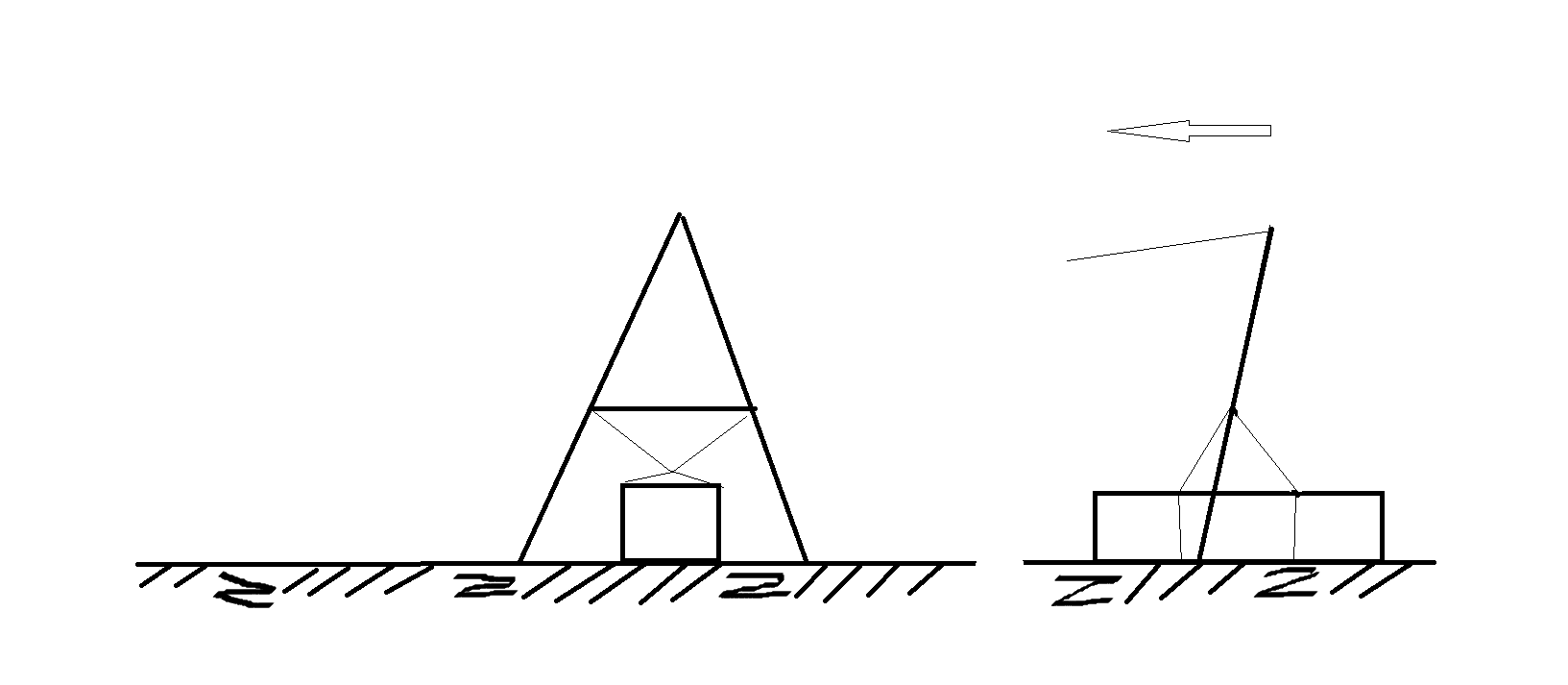
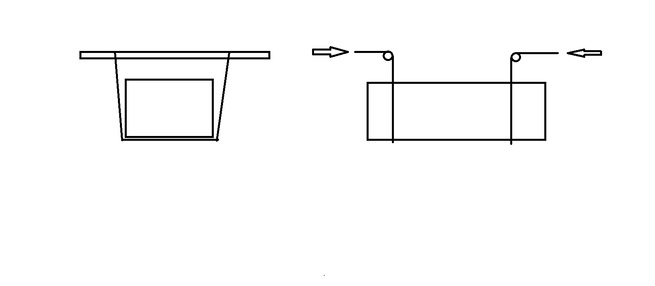
слева - вид на продольную ось дороги, справа - вид на поперечную ось.

Подробнее о технологии передвижки  на  https://cont.ws/@gladkoov.pave...

Рассмотрим расчет усилий, возникающих при передвижке каменного блока весом 3 т. Перекладина находится на половине высоты циркуля.

H = 2h

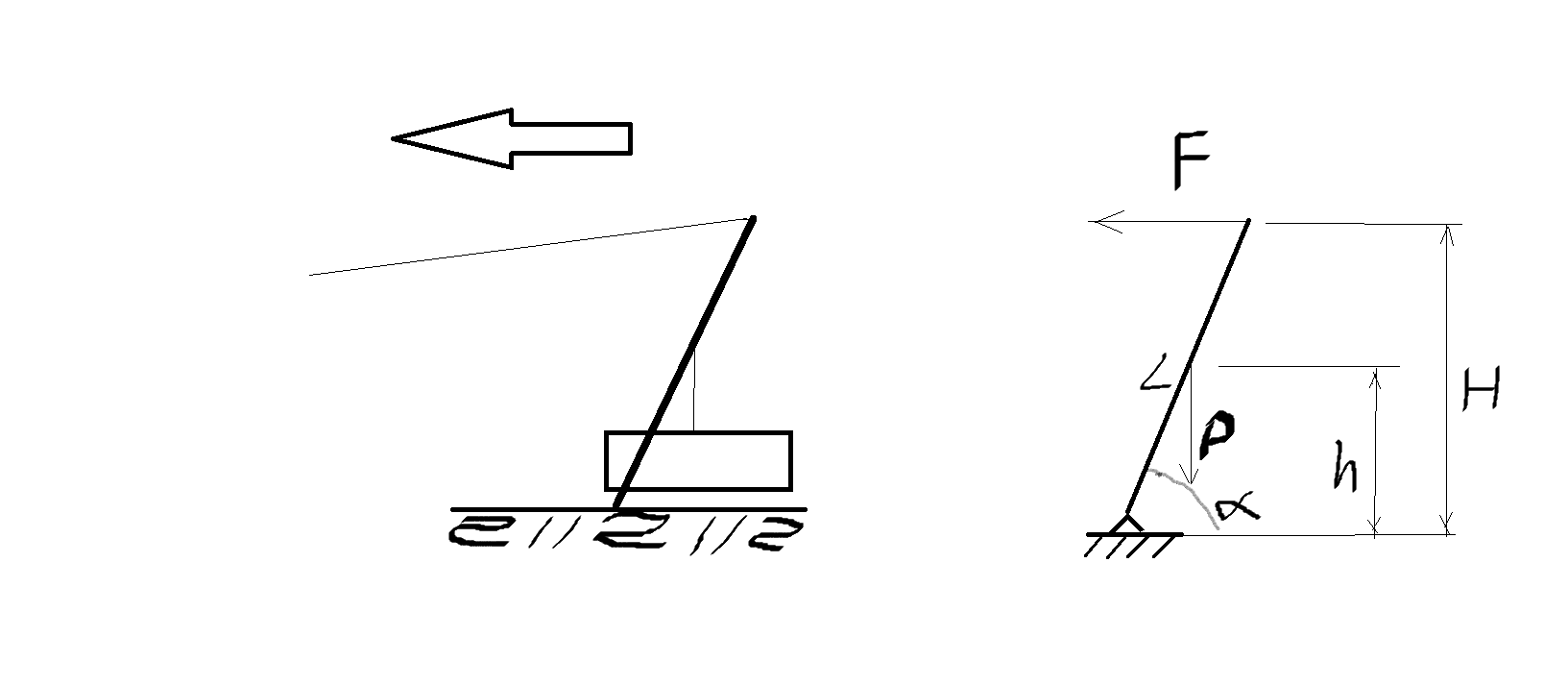
Из условия равновесия моментов сил получаем

F H = P h  ctg  а  или F = (Ph ctg a)/H - в общем случае

здесь а - угол альфа. F - горизонтальная составляющая тяги, Р - вес блока, h - высота подвески блока к циркулю. 

Анализ формулы показывает, что чем выше циркуль, чем ниже высота крепления блока, и чем меньше угол наклона, тем меньше тяговое усилие.

Расчет конкретного примера:

Масса блока  3 000кг, высоты циркуля  6 метров, высоты подвески 3 метра и угла наклона  в 85 град.

F = 3000 х ctg 85 град/2 = 3000 х 0,0875 /2 = 131 кг

При а = 2,5 град усилие 65 кг.  

Какое перемещение может сделать блок за один цикл?

S = L sin 5 град= 6 х 0,0872 = 0,523 м

Маловато.   Тем более, реальное перемещение будет меньше из-за пружинения каната подвески и увеличения из-за этого высоты подвески h. Поэтому увеличим размеры циркуля до высоты 12 м, высоту подвески до 6 м. Усилия при этом не изменятся,если пренебречь весом циркуля, а перемещение увеличится в два раза. Размеры самого устройства пока тоже достаточно реальные. Округляем и принимаем перемещение равным 1 метр, тягу так же округляем и принимаем 150 кг. Все эти округления создают нам некоторый запас для непредвиденных потерь.

Усилие тяги может быть горизонтальным, если тянущие залезут на пирамиду, что довольно просто сделать.

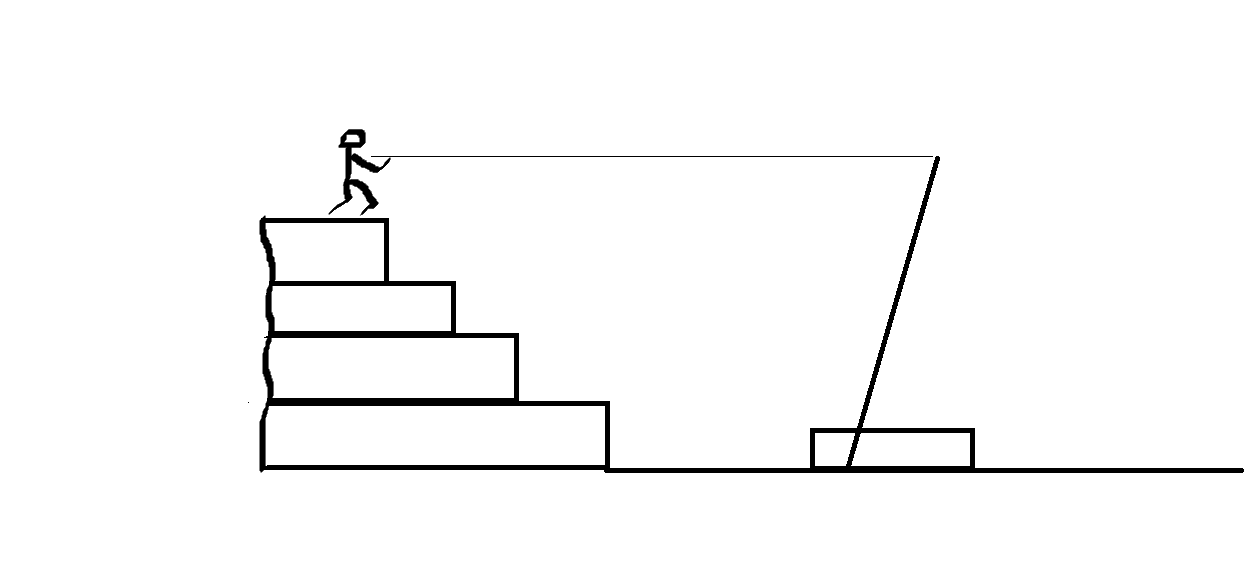
В итоге семь человек достаточно легко передвинут блок в 3 тонны весом на 1 метр за десять-пятнадцать секунд, если пренебречь временем перестановки циркуля. Если пирамида далеко, то увеличение усилия тяги спишем на пресловутые непредвиденные потери.

Теперь о потерях энергии. Блок идет по воздуху, ноги циркуля стоят на месте, но меняют угол наклона - то есть происходит трение качения.

Вычислим ситу трения качения по формуле

F = kР/R   у нас R = L

Для мягкого дерева k = 1.5 мм.  L = 12 м или 12000мм

F  =  1.5  х 3000/ 12000 = 0,375 кг. Ничтожная величина по сравнению с 150 кг тяги, но это и не удивительно для малого угла поворота и большого радиуса перекатывания.

Усилие тяги в 150 кг - максимальное при угле наклона в 85 град, когда циркуль встанет вертикально, он станет равным нулю, а затем тяга не нужна, блок сам будет поворачивать циркуль силой своей тяжести.

То есть на пути в первые полметра сила плавно понижается со 150 кг до нуля, а вторые полметра сопротивления движения нет. Хотя сила первые полметра изменяется по графику котангенса, упростим процесс, и будем считать, что изменение идет по закону прямой пропорциональности от 150 до 0. 

То есть  (150 + 0)/ 2  = 75 кг - средняя тяга на пути в первые полметра, на полном пути в 1 метр средняя тяга 37,5 кг.

Итак за полный цикл перемещения нужна тяга на увеличение потенциальной энергии в 37,5 кг и тяга на преодоление сопротивления качению в 0,375 кг. Прибавим встречный ветер и округлим результирующую силу до 40 кг.

В итоге КПД равен (3000-40)/3000=0,987 или 98,7 %

Для общего развития сравним КПД движения блока на деревянных катках из того же дерева диаметром 20 см. Допустим, что катки расположены  идеально перпендикулярно направлению движения, и при горизонтальном движении идет чистое качение.

Опять F = kР/R

Для мягкого дерева k = 1.5 мм. У нас здесь R = 0.5 D = 100 мм

F = 1.5 х 3000/ 100 = 45 кг, то есть при идеальных условиях катки диаметром 20 см дают почти такое же сопротивление, что и "египетский циркуль" высотой 12 м.

Но у циркуля есть резерв.

В случае, если мы не будем переставлять его по ходу движения за блоком, есть возможность по всему пути следования установить ряд таких циркулей на расстоянии друг от друга в один метр (длина одного цикла перемещения). Затем мы связываем канатом верхушки циркулей так, чтобы при вертикальном положении первого циркуля канат начинал бы тянуть следующий, то есть длина канатов между верхушками - полтора метра. Пусть угол отклонения будет все те же пять градусов.

В результате, когда рабочие натянут канат так, чтобы первый циркуль встал в вертикальное положение, им придется поднапрячься, чтобы через канат между первым и вторым циркулями начать поднимать и второй. Когда угол отклонения первого достигнет 2,5 град, угол второго будет также 2,5 град. В этом случае силы уравновесятся, и первый блок будет по инерции тянуть второй, причем дальше сила тяги будет нарастать даже без участия рабочих, используя потенциальную энергию высоты подъема первого блока. И вот эта потенциальная энергия будет переходить от одного блока к другому и дальше к следующему, теряясь минимально лишь на трение качения.

И вот наступает эффект падающего домино: каждый блок тянет за собой следующий, и при равенстве весов блоков и горизонтальной поверхности дороги можно поставить сотни (или тысячи?) циркулей, но по-настоящему поднимать лишь первые два, а дальше поддерживать процесс, компенсируя лишь потери на качание устройств.

Тут и наступает момент, когда  КПД многочисленного ряда циркулей приближается к умопомрачительным цифрам.

Ведь на один  цикл движения сопротивление качению равно 0,375 кг, даже если увеличить его до 1 кг, КПД длинной дороги из египетских циркулей может быть

(3000 - 1)/ 3000 = 0,9997 или 99,97 %. Почти сто процентов приложенной людьми энергии такие устройства превращают в энергию движения. Нужна лишь пара человек на каждые десять устройств, чтобы компенсировать потери на качение, и все те же семь-десять человек на первоначальный импульс.

Но в реальности путь от Нила, по которому привезли блоки, к подножию пирамиды идет на подъем. Поэтому людей понадобится больше, хотя КПД от этого не изменится. А путь от каменоломен к Нилу идет вниз, здесь для силового импульса на всю вереницу блоков вот эти десять человек и нужны. Дальше только тормози. При этом дорога может быть не очень ровной , иметь повороты и меняющийся уклон.

Это вам не катки с горизонтальной поверхностью или равномерным уклоном без поворотов.

 Фантастика?

Конечно фантастика, но вся закавыка лишь в плане того, что по окончании каждого цикла нужно отвязать канаты от блоков, а также вернуть сами циркули в исходное положение, после чего перебросить канаты подвески от предыдущего блока к последующему. И так после каждого цикла :

- рычаги имеют высокий КПД, но малый цикл перемещений.

Но и, пожалуй, стоит еще раз подчеркнуть, что все эти процессы не противоречат законам физики, очень банальны, они реально под силу людям древности, но происходили ли они на самом деле - пока неизвестно. Статья лишь формирует вектор поисков:

- папирусы и раскопки, рисунки и прочее.

П. Гладков