Частенько в сети возникают споры на околокосмические темы, люди в попытках понять самим или доказать оппонентам спорят – мы в .опе или еще/уже нет? Если да, то насколько глубока она эта, как её….
Одни в спорах утверждают - смотрите! У нас ого-го!!!. Другие не отстают - глядите, да они эге-гей!!! Такие споры, как правило заканчиваются ничем, поскольку большинство спорщиков имеют весьма отдаленное представление о предмете спора.
Одному человеку знать всё, что связано с космическими технологиями невозможно, но общее представление иметь – было бы неплохо. И я сделаю попытку вооружить именно общим представлением о ракетно-космических технологиях тех, кому будет интересно или захочется пофлудить на околокосмическую тематику.
Ракете нужен ракетный двигатель – это не обсуждается. Нужен двигатель с необходимой тягой и экономичностью. Всем понятно, что чем экономичнее двигатель, тем лучше, и ракетный двигатель – не исключение.
Понятие экономичности для ракетного двигателя - несколько иное, нежели для автомобильного. Строго говоря - то, как определяется экономичность двигателя - зависит от его назначения.Если автомобиль предназначен для перемещения на расстояние – то за показатель экономичности принимается расход топлива на пройденное расстояние, если двигатель предназначен генерации мощности, то показателем экономичности будет расход топлива на единицу генерируемой мощности.
Что же касается ракетного двигателя – то его задача создавать тягу.
Логично, что, поскольку тяга для ракетного двигателя – это главный целевой показатель, то основным показателем экономичности ракетного двигателя принято считать расход топлива на единицу создаваемой тяги, а точнее – обратную величину, называемую удельным импульсом
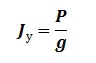
где P – тяга двигателя в ньютонах, а g – расход топлива в килограммах в секунду. Измеряется он в ньютонах, помноженных на секунду и деленных на килограмм (или ньютонах, деленных на килограмм в секунду) [н*с/кг].
У тех людей, которые тягу измеряют в килограммах (тоннах), удельный импульс измеряется в секундах. Но мы то с вами знаем, что в килограммах измеряется масса, а значит и как все нормальные люди будем измерять удельный импульс в [н*с/кг] или в [м/с].
Метры в секунду получаются путем сокращения размерностей, и из этого становится понятен физический смысл удельного импульса - это по сути «эффективная» скорость истечения реактивной струи.
Чем более высокую скорость имеет реактивная струя, тем двигатель экономичнее.
Теперь стоит разобраться в том, чем же экономичность, например, автомобильного двигателя отличается от экономичности ракетного.
Если говорить об экономичности автомобильного двигателя, то все просто – двигатель автомобиля, когда тот проедет нужное расстояние, израсходует какое-то количество топлива. В полтора раза более экономичный двигатель израсходует в полтора раза меньше топлива, вдвое более экономичный – вдвое меньше топлива и т.д.
Работа, затрачиваемая на движение автомобиля, практически не зависит от массы топлива, заправленного в баке (что такое разница в массе топлива 20-30 кг при массе автомобиля больше тонны?).
Именно эта причина делает экономичность ракетного двигателя критически важной характеристикой, поскольку масса топлива, которое сжигают ракеты в полете составляет значительную часть массы всей ракеты. Иными словами – ракета перемещает вместе с собой в большей степени топливо, чем полезный груз и собственную конструкцию.
Просто представьте – при ухудшении экономичности автомобильного двигателя на 10% - просто берем и заправляем на 10% больше топлива, а при ухудшении экономичности ракетного двигателя на 10% - такого же увеличения запаса топлива хватило бы только на имеющуюся массу ракеты, но ведь масса ракеты тоже увеличилась, а значит 10-ти %-ного увеличения массы топлива уже недостаточно.
Чтобы получить количественные оценки влияния экономичности ракетного двигателя на необходимые запасы ракетного топлива нужно обратиться к формуле Циолковского:
Скорость, которую может приобрести ракета по окончании работы двигателя, зависит от удельного импульса и логарифма отношения массы полной ракеты к массе пустой ракеты.
Для вывода ракеты, допустим на орбиту, ей помимо достижения космической скорости, необходимо преодолеть гравитационное притяжение земли, сопротивление воздуха, набрать высоту, и по ходу траектории осуществлять управляющие действия.
Все эти составляющие принято выражать через потери скорости на гравитацию, сопротивление воздуха e.t.c.. Эти потери скорости и необходимую скорость суммируют и называют потребной «характеристической скоростью».
Для вывода на орбиту, ракетный двигатель должен иметь возможность сообщить ракете эту самую характеристическую скорость. Характеристическую скорость можно посчитать, зная параметры орбиты и траектории вывода на эту орбиту. Скорость эта ощутимо больше, чем, например, первая космическая. Для вывода на низкую орбиту можно, не сильно ошибившись, принять потребную характеристическую скорость 9100 м/с.
Из формулы Циолковского можно вывести обратное уравнение
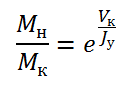
Это уравнение говорит о том, что отношение масс полной и пустой ракеты экспоненциально зависит от отношения требуемой характеристической скорости ракеты к удельному импульсу.
Если предположить, что характеристическая скорость, нужная для вывода на орбиту известна, то при некотором удельном импульсе двигателя, масса полной ракеты должна быть больше массы пустой в какое-то количество раз. И если удельный импульс двигателя будет меньше, скажем в 1,2 раза, то отношение масс должно вырасти уже в 1,2214 раза.
Теперь давайте возьмем цифры, близкие к реальности, и посчитаем.
В качестве исходных данных:
- потребная для вывода на орбиту (характеристическая) скорость – 9100 м/с
- удельный импульс – 3000 м/с
- стартовая масса (полной) ракеты – 100 тонн.
В этом случае отношение масс полной и пустой ракеты получится 20,8
соответственно масса ракеты в момент окончания работы двигателя, когда израсходуется все топливо, будет 4,8 тонны.
Это говорит о том, что для того, чтобы достичь нужной скорости, ракете с таким удельным импульсом нужно иметь топлива на борту в количестве не менее 95,2 % от полной массы ракеты.
Казалось бы – ну и что? Заливаем нужное количество топлива и алга!
А дело в том, что в оставшиеся 4,8 % массы нужно уместить и конструкцию ракеты, и двигатель, и полезный груз.
В настоящее время, в среднем по больнице, в космических ракетах около 8% массы – это масса двигателя и конструкции самой ракеты, которые никак не умещаются в отведенные физикой 4,8%!
Иными словами - с таким удельным импульсом ракета не сможет вывести на орбиту не только полезный груз, но и себя любимую.
Теперь давайте посмотрим - как поменяется ситуация, в случае наличия двигателя с более высоким удельным импульсом, при всё той же стартовой массе 100 тонн.
Расчеты приводить не буду, дабы не загромождать, дам только итоговые цифры:
при удельном импульсе 3500 м/с – топлива требуется 92,58% стартовой массы, конечная масса – 7,42 тонны – это уже почти хватает на то чтобы без груза выйти на орбиту
при удельном импульсе 3700 м/с – топлива требуется 91,46% стартовой массы, конечная масса – 8,54 тонны – можно уже пол тонны (0,54) с собой прихватить
а при удельном импульсе 4000 м/с – топлива требуется 89,73% стартовой массы, конечная масса 10,27 тонны. Вычитаем 8 тонн массы самой ракеты, и остается 2,27 тонны свободного места для полезного груза.
Только представьте – удельный импульс вырос с 3700 до 4000 - всего на 8,1 %, а масса полезного груза – в 4,2 раза!
Все вышеприведенные рассуждения, хоть и построены вокруг одноступенчатой ракеты, но также справедливы и для двух- и более ступенчатых ракет. Двухступенчатые ракеты позволяют выводить грузы на орбиту с двигателями, имеющими существенно меньший удельный импульс.
Чтобы наглядно продемонстрировать влияние удельного импульса двигателей на эффективность ракеты-носителя - предлагаю взглянуть на такую картинку, которая говорит, о том, какова должна быть стартовая масса абстрактной двухступенчатой ракеты, предназначенной для вывода на орбиту одной тонны полезного груза при различных значениях удельного импульса:
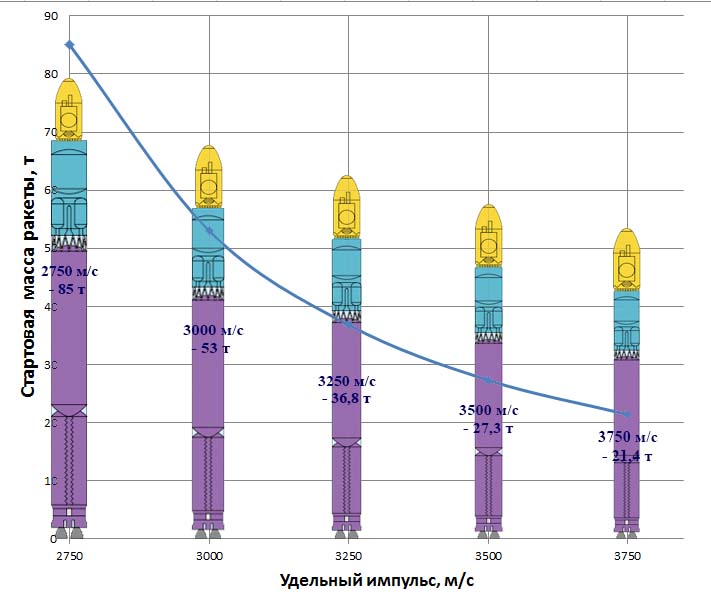
Ну, или так:
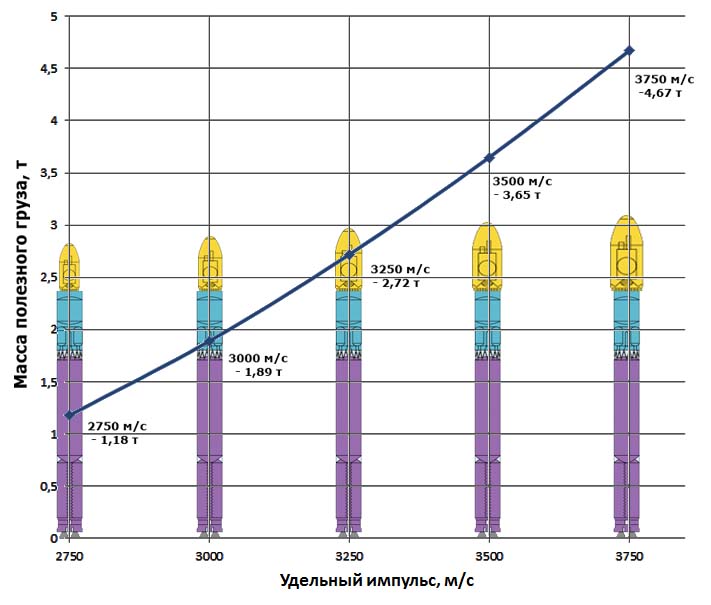
здесь видно, как изменяются возможности по выводу на орбиту груза абстрактной двухступенчатой ракетой, имеющей стартовую массу 100 тонн в зависимости от удельного импульса.
Относительно скромный прирост экономичности ракетного двигателя приводит к существенному сокращению её массо-габаритных параметров при фиксированной массе полезного груза, либо существенно увеличивает её возможности по выводу полезного груза на орбиту при фиксированной стартовой массе.
Вот это и есть главная причина, по которой конструкторы ракетных двигателей бьются за каждую долю процента повышения удельного импульса.
О том, какими путями конструкторы ракетных двигателей ходят, пытаясь добиться максимально возможного удельного импульса двигателей – я расскажу в следующих частях.
-
-
- +1
-
Зачем поддерживать автора?
Зачем поддерживать автора?
- - Любой текст это труд, если вам понравилась статья, то поддерживая автора - вы показываете, что оценили то, что он потратил свое время и силы.
- - Автор получает небольшую финансовую помощь от вас, у него появляется больше стимула сделать еще лучше.
- - Статья, которую поддерживают пользователи попадет в рейтинг по поддержке на главной странице Конта, что принесет ей больше просмотров и откликов, а значит, поддерживая статью вы помогаете автору продвигать его точку зрения.
Оценили 35 человек
45 кармы