Эволюция НАШЕГО образования за 30 лет (1980-е -- 2010-е)

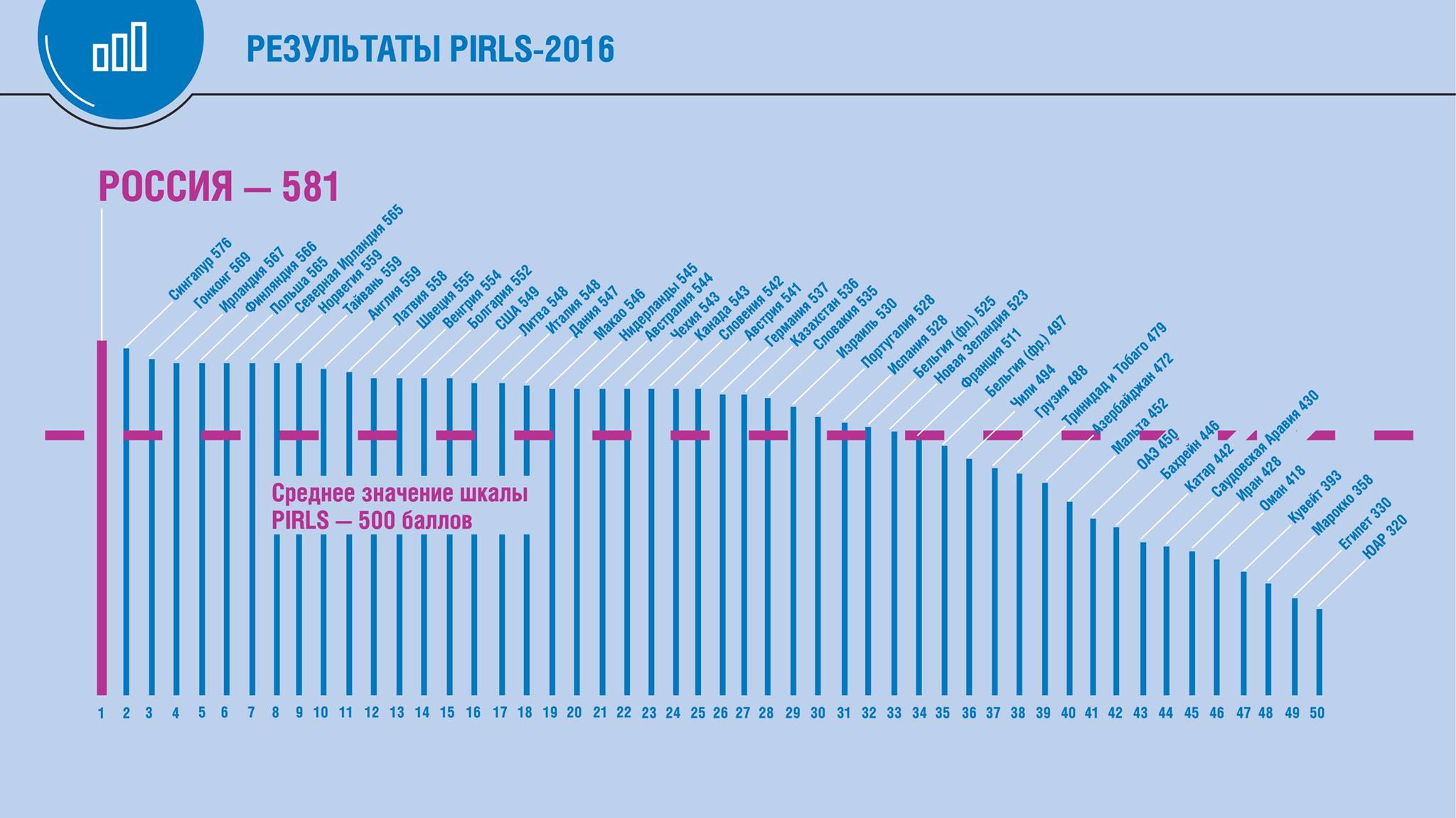
Попробовал дать некоторое представление об уровне образования в СССР 80-х годов в сравнении с уровнем образования в России после 2010 года, на основе сравнения Государственных выпускных экзаменов за неполную среднюю школу. Преподавателям вузов настоятельно советую не забывать, что рождаемость в СССР была выше в несколько раз, чем в России ( 1960 -- 5350000 ; 1999 -- 1210000). Иными словами раньше вузы имели дело исключительно со "сливками", а сейчас с массой, прошедшей примитивный порог современного ЕГЭ.

Экзаменационная работа 1989 года за неполную среднюю школу (100% заданий):

1. Расположите числовые выражения в порядке возрастания их значений

-3/7*0,432 ; -0,112:5/9 ; 0,477- 2/3 ;

2. При каких значениях х выражение‎ имеет смысл: √(х^2 - 2х + 3)

3. Упростите выражение: (ctgπ/6 sinπ/6)/cosπ/3

4. Катер прошел 8 км по течению реки и 16 км против течения,затратив на весь путь 4/3 ч. Какова скорость движения катера по течению,если собственная скорость катера равня 20 км/ч?

5. Первое число равно 1,8, второе 1,2. Сколько процентов первое число составляет от суммы этих чисел? На сколько процентов первое число больше второго? На сколько процентов второе меньше первого?

Экзаменационная работа 2018 года за неполную среднюю школу (19% заданий ОГЭ):

1. Установите соответствие между графиками функций и формулами, которые их задают. ГРАФИКИ .....(можно посмотреть по ссылке.) ФОРМУЛЫ:А) y=х^2 Б) у=x/2 В) y=2/х В таблице под каждой буквой укажите соответствующий номер.

2. Укажите решение системы неравенств: х+2,6<0 и х+5>1 (выбрать из четырёх вариантов)

3. Найдите площадь трапеции, изображённой на рисунке.

4. Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?

5. Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжений боковых сторон треугольника и касается основания AC . Найдите радиус окружности, вписанной в треугольник ABC .

Экзаменационная работа 1989 года за неполную среднюю школу.

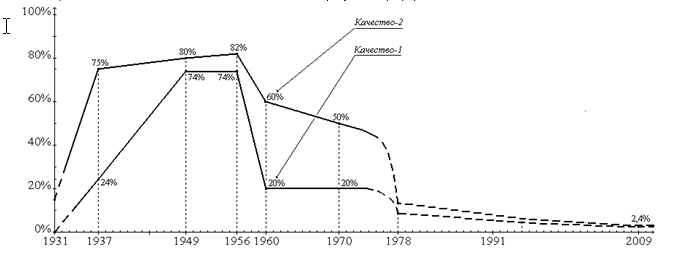
Как известно, к 1980 году уровень школьного образования окончательно рухнул: https://cont.ws/@mikluho/1532695

Начиная с 1982 года экзамен за неполную среднюю школу в СССР проходил по заранее известным заданиям. Огромными тиражами выпускалась брошюра: Сборник задач и упражнений для проведения письменного экзамена по математике в восьмых классах общеобразовательных школ РСФСР: Министерство просвещения РСФСР.- М.: Просвещение, 1981, -65 с. В сборнике 450 номеров для первого варианта и 450 номеров для второго.

5 заданий для экзаменационной работы выбирались из этих задач, без каких либо изменений.

Мои впечатления о том славном времени:

Перспектива сдавать экзамены по алгебре навевала скуку. А что если?

11 января ребята вышли на учёбу после каникул. Я сделал им предложение, от которого они не захотели отказываться.

В то время экзамены в 9 классе проводились по стандартному набору заданий. Я предложил прорешать в течении 3 четверти эти 450 номеров.

Ребята согласились. Работа закипела. Из каждого раздела сборника первое задание делали на доске, а остальные самостоятельно. Получить для проверки 16650 номеров дополнительно? Перспектива не радовала. Эврика!

В сорока пяти ученических тетрадях, исписанных мной, приведены решения всех (900) заданий. Я решал их 45 дней по 20 номеров в день. Ребята самостоятельно проверяли свои решения по этим "решебникам", а решебников ещё не существовало - появились позже. Приблизительно треть учеников прорешали задания полностью, 1/3, основательно проработав все разделы, сознательно ограничились 300 - 400 заданиями, а остальные сделали менее 300, уделяя особое внимание необходимым разделам. Последние сознательно не стремились к пятёркам.

В конечном итоге экзамен формально превратился в релейную работу. Решать нужно было знакомые номера. Не удивительно, что через полтора часа ( из трёх) в классе практически никого не осталось. Через три часа в параллельных классах только начали сдавать работы.

За решение всей работы выставляется оценка по следующим правилам:

Оценка “5”, если все задания выполнены без ошибок, причем работа может содержать не более двух недочетов;

Оценка “4” выставляется в следующих случаях:

а) если все задания выполнены без ошибок, причем работа содержит более двух недочетов;

б) если решены без ошибок четыре задания, среди которых имеется текстовая задача;

в) если решены без недочётов четыре задания, в которые не вошла текстовая задача;

Оценка “3” выставляется, если решены без ошибок три задания.

Оценка “2” выставляется, если решены верно только два задания.

К ошибкам относятся погрешности, которые обнаруживают незнание учащимися формул, правил, основных свойств и неумение их применять, потеря корня или сохранение постороннего корня в ответе, неумение строить и читать графики функций в объеме программных требований, а также вычислительные ошибки, если они не являются опиской.

К недочетам относятся: описки; ошибки в записи ответа; недостаточность или отсутствие необходимых теоретических преобразований; нерациональное решение.

Согласно жеребьёвке, проведённой центробанком (https://cont.ws/@mikluho/1310151, )в работу, представленную выше, вошли:

Номер 78 из первого раздела ; номер 79 из второго ; 79 из третьего ; 67 и 70 из 4 и 5 соответственно. (Нумерация в сборнике соответственно: 78 ; 169 ; 259 ; 337 ; 430)

Экзаменационная работа 2018 года за неполную среднюю школу.

Современный экзамен включает в себя 26 заданий. Существуют и пособия для подготовки к этим экзаменам. Их несколько, самый престижный: "Ященко. ОГЭ-2020. Математика. 36 вариантов. Типовые экзаменационные варианты. ФИПИ." 36*26=936 номеров. Многие скажут: велика ли разница 450 или 936? Однако, разница совсем в другом.

Восьмиклассникам СССР гарантировалось полное совпадение 100% номеров.

Современный выпускник таких шансов лишен напрочь, хотя аналогичные задания ему попадутся (оценочно 30%).

Существует открытый банк заданий ФИПИ http://www.fipi.ru/content/otkrytyy-bank-zadaniy-oge из которого набирают первые 20 заданий. Я насчитал в нём 5079 заданий.

Велика ли разница: 450 или 5079?

Представление об экзамене можно получить рассматривая Демонстрационный вариант 2018 года. https://4ege.ru/gia-matematika/55303-demoversiya-oge-2018-po-matematike.html

В статье представлены пять из 26 задач ОГЭ этого демонстрационного варианта. Центробанк снова помог выбрать задания ( https://cont.ws/@mikluho/1527180 ): 2 ; 6 ; 10 ; 14 ; 18 ; 22 ; 26. (Два первых оставил за скобками, чтобы уравнять количество.)

Работа состоит из двух модулей: «Алгебра» и «Геометрия». Всего в работе 26 заданий. Модуль «Алгебра» содержит семнадцать заданий: в части 1 — четырнадцать заданий; в части 2 — три задания. Модуль «Геометрия» содержит девять заданий: в части 1 — шесть заданий; в части 2 — три задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Шкала пересчета баллов ОГЭ 2018 в оценки - Математика.

0—7 баллов — отметка «2»

8—14 баллов — отметка «3»

15—21 баллов — отметка «4»

22—32 баллов — отметка «5»

(при условии, что из них не менее 2 баллов получено по модулю «Геометрия».)

Важно отметить, что в СССР ученики сидели по двое за столом. Варианты у них были до безобразия аналогичными. Учителя специально сажали сильных учеников со слабыми. Очень часто для всего класса и учителей закупались абсолютно одинаковые ручки.

В России ученики сидят строго по одному. Ведётся видеозапись экзамена. Количество вариантов сильно превышает 2.

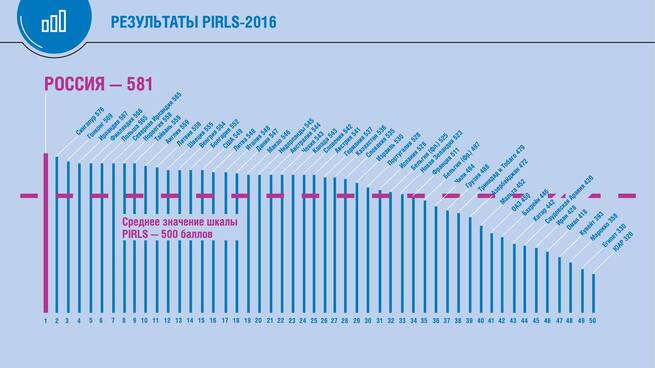
Как результат: беспрецедентная динамика повышения уровня школьного образования в России. https://cont.ws/@mikluho/87927...